
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 与
与![]() 的交点坐标;
的交点坐标;
(2)过曲线![]() 上任一点
上任一点![]() 作与
作与![]() 夹角为30°的直线,交
夹角为30°的直线,交![]() 于点
于点![]() ,且
,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】斐波那契数列0,1,1,2,3,5,8,13,…,是意大利数学家列昂纳多·斐波那契发明的,定义如下:![]() ,
,![]() ,
,![]() .某同学设计了一个求解斐波那契数列前
.某同学设计了一个求解斐波那契数列前![]() 项和的程序框图,如图所示,若输出
项和的程序框图,如图所示,若输出![]() 的值为232,则处理框和判断框中应该分别填入( )
的值为232,则处理框和判断框中应该分别填入( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科站技术员为了解某品种树苗的生长情况,在该批树苗中随机抽取一个容量为100的样本,测量树苗高度(单位:cm).经统计,高度均在区间[20,50]内,将其按[20,25),[25,30),[30,35),[35,40),[40,45),[45,50]分成6组,制成如图所示的频率分布直方图,其中高度不低于40cm的树苗为优质树苗.
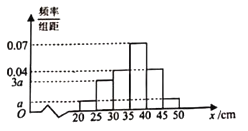
(1)已知所抽取的这100棵树苗来自于甲、乙两个地区,部分数据如下2×2列联表所示,将列联表补充完整,并根据列联表判断是否有99.9%的把握认为优质树苗与地区有关?
(2)用样本估计总体的方式,从这批树苗中随机抽取4棵,期中优质树苗的棵数记为X,求X的分布列和数学期望.
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
附:K2=![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年由于猪肉涨价太多,更多市民选择购买鸡肉、鸭肉、鱼肉等其它肉类.某天在市场中随机抽出100名市民调查,其中不买猪肉的人有30位,买了肉的人有90位,买猪肉且买其它肉的人共30位,则这一天该市只买猪肉的人数与全市人数的比值的估计值为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“我将来要当一名麦田里的守望者,有那么一群孩子在一块麦田里玩,几千万的小孩子,附近没有一个大人,我是说……除了我”《麦田里的守望者》中的主人公霍尔顿将自己的精神生活寄托于那广阔无垠的麦田.假设霍尔顿在一块成凸四边形![]() 的麦田里成为守望者,如图所示,为了分割麦田,他将
的麦田里成为守望者,如图所示,为了分割麦田,他将![]() 连接,设
连接,设![]() 中边
中边![]() 所对的角为
所对的角为![]() ,
,![]() 中边
中边![]() 所对的角为
所对的角为![]() ,经测量已知
,经测量已知![]() ,
,![]() .
.

(1)霍尔顿发现无论![]() 多长,
多长,![]() 为一个定值,请你验证霍尔顿的结论,并求出这个定值;
为一个定值,请你验证霍尔顿的结论,并求出这个定值;
(2)霍尔顿发现麦田的生长于土地面积的平方呈正相关,记![]() 与
与![]() 的面积分别为
的面积分别为![]() 和
和![]() ,为了更好地规划麦田,请你帮助霍尔顿求出
,为了更好地规划麦田,请你帮助霍尔顿求出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com