
如图,过四棱柱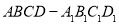 形木块上底面内的一点
形木块上底面内的一点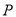 和下底面的对角线
和下底面的对角线 将木块锯开,得到截面
将木块锯开,得到截面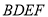 .
.
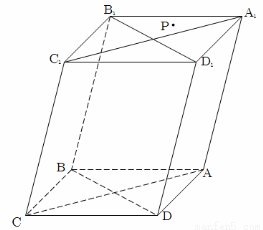
(1)请在木块的上表面作出过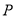 的锯线
的锯线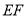 ,并说明理由;
,并说明理由;
(2)若该四棱柱的底面为菱形,四边形时矩形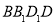 ,试证明:平面
,试证明:平面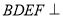 平面
平面 .
.
(1)如图 (2)详见解析
【解析】
试题分析:(1)本题实质为确定截面与上底面的交线,这利用面面平行性质定理,可得交线相互平行:即由平面ABCD//平面A1B1C1D1,平面BDFE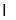 平面ABCD=BD,平面BDFE
平面ABCD=BD,平面BDFE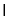 平面A1B1C1D1=EF,得EF//BD,又 B1B//D1D,从而EF// B1D1 (2)证明面面垂直,一般利用其判定定理,即证线面垂直:由BD
平面A1B1C1D1=EF,得EF//BD,又 B1B//D1D,从而EF// B1D1 (2)证明面面垂直,一般利用其判定定理,即证线面垂直:由BD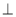 A1A,BD
A1A,BD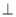 AC得到BD
AC得到BD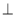 平面A1C1CA,从而平面BDFE
平面A1C1CA,从而平面BDFE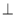 平面A1C1CA
平面A1C1CA
试题解析:(1)
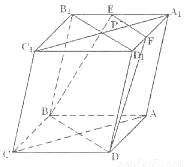
在上底面内过点P作B1D1的平行线分别交A1D1,A1B1于F,E两点,则EF为所作的锯线. 2分
在四棱柱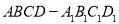 中,侧棱B1B//D1D,B1B=D1D,
中,侧棱B1B//D1D,B1B=D1D,
所以四边形BB1D1D是平行四边形,B1D1//BD 4分
又平面ABCD//平面A1B1C1D1,平面BDFE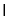 平面ABCD=BD,平面BDFE
平面ABCD=BD,平面BDFE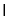 平面A1B1C1D1=EF,
平面A1B1C1D1=EF,
所以EF//BD,从而EF// B1D1 7分
(2) 证明:由于四边形BB1D1D是矩形,所以BD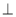 B1B,又A1A//B1B
B1B,又A1A//B1B
所以BD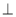 A1A 9分
A1A 9分
又四棱柱的底面为菱形,所以BD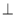 AC
AC
因为AC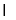 A1A=A,AC
A1A=A,AC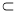 平面A1C1CA, A1A
平面A1C1CA, A1A 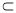 平面A1C1CA
平面A1C1CA
所以BD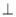 平面A1C1CA 12分
平面A1C1CA 12分
因为BD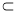 平面BDFE
平面BDFE
所以平面BDFE 平面A1C1CA 14分
平面A1C1CA 14分
考点:面面平行性质定理,面面垂直判定定理


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源:2014-2015学年山东省潍坊市高三上学期期末考试文科数学试卷B卷(解析版) 题型:解答题
某公司生产甲、乙两种桶装产品,已知生产甲产品1桶需耗A原料3千克,B原料1千克;生产乙产品1桶需耗A原料1千克,B原料3千克.每生产一桶甲产品的利润400元,每生产一桶乙产品的利润300元.公司在生产这两种产品的计划中,每天消耗A、B原料都不超过12千克,通过合理安排生产计划,公司每天可获得的最大利润是(单位:元)( )
A.1600 B.2100 C.2800 D.4800
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省济南市高三上学期期末考试理科数学试卷(解析版) 题型:填空题
已知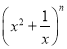 的二项展开式的各项系数和为32,则二项展开式中含
的二项展开式的各项系数和为32,则二项展开式中含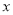 项的系数为________.
项的系数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com