
已知函数f(x)= x3+x2+ax+1(a∈R).
x3+x2+ax+1(a∈R).
(1)求函数f(x)的单调区间;
(2)当a<0时,试讨论是否存在x0∈(0,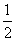 )∪(
)∪(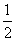 ,1),使得f(x0)=f(
,1),使得f(x0)=f(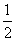 ).
).
解 (1)f′(x)=x2+2x+a开口向上,Δ=4-4a=4(1-a).
①当1-a≤0,即a≥1时,f′(x)≥0恒成立,f(x)在R上单调递增.
②当1-a>0时,即a<1时,令f′(x)=0,解得x1=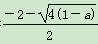 =-1-
=-1-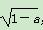 ,x2=-1+
,x2=-1+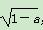 .
.
令f′(x)>0,解得x<-1-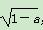 或x>-1+
或x>-1+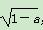 ;
;
令f′(x)<0,解得-1-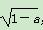 <x<-1+
<x<-1+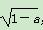 ;
;
所以f(x)的单调递增区间为(-∞,-1-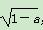 )和(-1+
)和(-1+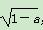 ,+∞);
,+∞);
f(x)的单调递减区间为(-1-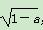 ,-1+
,-1+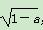 ).
).
综上所述:当a≥1时,f(x)在R上单调递增;当a<1时,f(x)的单调递增区间为(-∞,-1-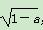 )和(-1+
)和(-1+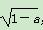 ,+∞),f(x)的单调递减区间为(-1-
,+∞),f(x)的单调递减区间为(-1-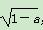 ,-1+
,-1+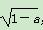 ).
).
(2)当a<0时,x1=-1-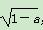 <0,x2=-1+
<0,x2=-1+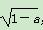 >0.
>0.
①当-1+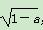 ≥1时,即a≤-3时,f(x)在(0,1)上单调递减,不满足题意;
≥1时,即a≤-3时,f(x)在(0,1)上单调递减,不满足题意;
②当-1+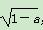 <1时,即-3<a<0时,f(x)在(0,-1+
<1时,即-3<a<0时,f(x)在(0,-1+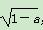 )上单调递减,在(-1+
)上单调递减,在(-1+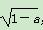 ,1)上单调递增,
,1)上单调递增,
所以f(x)min=f(-1+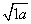 ),由题意知-1+
),由题意知-1+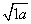 ≠
≠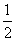 ,所以a≠-
,所以a≠-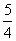 .
.
f(x)max=max{f(0),f(1)};f(0)=1,f(1)=a+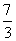 .
.
a.当a+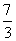 ≥1时,即-
≥1时,即-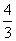 ≤a<0时,f(x)max=f(1).
≤a<0时,f(x)max=f(1).
令f(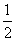 )<f(0),解得a<-
)<f(0),解得a<-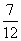 ,
,
又因为-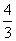 ≤a<0,所以-
≤a<0,所以-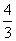 ≤a<-
≤a<-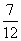 且a≠-
且a≠-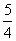 .
.
b.当a+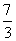 <1时,即a<-
<1时,即a<-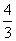 时,f(x)max=f(0).
时,f(x)max=f(0).
令f(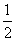 )<f(1),解得-
)<f(1),解得-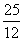 <a<-
<a<-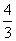 .
.
综上所述,当a∈{a|-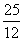 <a<-
<a<-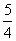 或-
或-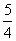 <a<-
<a<-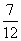 }时,存在x0∈(0,
}时,存在x0∈(0,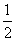 )∪(
)∪(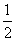 ,1),使得f(x0)=f(
,1),使得f(x0)=f(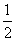 ).
).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知集合A={x|y=lg(x-x2)},B={x|x2-cx<0,c>0},若A⊆B,则实数c的取值范围是( )
A.(0,1] B.[1,+∞)
C.(0,1) D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
某班共30人,其中15人喜爱篮球,10人喜爱乒乓球,8人对这两项运动都不喜爱,则喜爱篮球但不喜爱乒乓球的人数为( )
A.11人 B.12人 C.13人 D.14人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com