
分析 利用倍角公式降幂,再用两角和的正弦化积,由相位的终边落在y轴上求得x值得答案.
解答 解:f(x)=sin2x-sinxcosx=$\frac{1-cos2x}{2}-\frac{1}{2}sin2x$
=$-\frac{\sqrt{2}}{2}sin(2x+\frac{π}{4})+\frac{1}{2}$.
由$2x+\frac{π}{4}=\frac{π}{2}+kπ$,得x=$\frac{π}{8}+\frac{kπ}{2},k∈Z$.
取k=0,得x=$\frac{π}{8}$.
∴与原点距离最小的对称轴方程是x=$\frac{π}{8}$.
故答案为:x=$\frac{π}{8}$.
点评 本题考查三角函数的恒等变换应用,考查y=Asin(ωx+φ)型函数的图象和性质,是基础题.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (4,+∞) | C. | (-∞,4] | D. | (-∞,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{1-{k}^{2}}}{k}$ | B. | -$\frac{\sqrt{1-{k}^{2}}}{k}$ | C. | $\frac{k}{\sqrt{1-{k}^{2}}}$ | D. | -$\frac{k}{\sqrt{1-{k}^{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | ($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$) | C. | ($\overrightarrow{a}$+$\overrightarrow{b}$)∥($\overrightarrow{a}$-$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
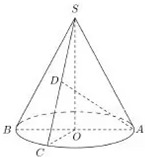 如图,在圆锥SO中,AB为底面圆O的直径,点C为弧$\widehat{AB}$的中点,SO=AB;
如图,在圆锥SO中,AB为底面圆O的直径,点C为弧$\widehat{AB}$的中点,SO=AB;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | $\frac{4\sqrt{2}}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
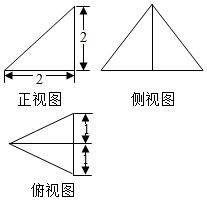
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$$\sqrt{2}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com