
分析 (1)设x1、x2是R上任意两个值,且x1<x2,求得∴f(x1)-f(x2)<0,可得f(x)在R上是增函数.
(2)先证明f(x)为奇函数,不等式即f(3)>-f(2a-a2)=f(a2-2a),再利用f(x)在R上是增函数 可得a2-2a<3,由此求得a的范围.
(3)利用f(x)的单调性求得A,设g(x)在[-1,1]上的值域为B,则由题意可知A⊆B,分类讨论求得B,从而求得实数m的取值范围.
解答 解:(1)证明:f(x)的定义域为R,设x1、x2是R上任意两个值,且x1<x2,则$f({x_1})-f({x_2})=1-\frac{2}{{{2^{x_1}}+1}}-(1-\frac{2}{{{2^{x_2}}+1}})=\frac{{2({2^{x_1}}-{2^{x_2}})}}{{({2^{x_1}}+1)({2^{x_2}}+1)}}$,
∵x1<x2,∴${2^{x_1}}>0$,${2^{x_2}}>0$,${2^{x_1}}<{2^{x_2}}$,∴f(x1)-f(x2)<0,
∴f(x)在R上是增函数.
(2)∵$f(-x)=\frac{{{2^{-x}}-1}}{{{2^{-x}}+1}}=\frac{{\frac{1}{2^x}-1}}{{\frac{1}{2^x}+1}}=\frac{{1-{2^x}}}{{1+{2^x}}}=-f(x)$,∴f(x)在R上是奇函数,
∵f(2a-a2)+f(3)>0,∴f(3)>-f(2a-a2)=f(a2-2a),
又∵f(x)在R上是增函数,∴a2-2a<3,
解得-1<a<3,∴所求实数a构成的集合为 {a|-1<a<3}.
(3)∵f(x)在R上是增函数,∴当x1∈[-1,1]时,f(x1)∈[f(-1),f(1)],即$f({x_1})∈[-\frac{1}{3},\frac{1}{3}]=A$.
设g(x)在[-1,1]上的值域为B,则由题意可知A⊆B.
∵$g(x)={(x+m)^2}+\frac{5}{3}-{m^2}$,∴$\frac{5}{3}-{m^2}≤-\frac{1}{3}$,解得 $m≤-\sqrt{2}$或$m≥\sqrt{2}$,
①当$m≤-\sqrt{2}$时,函数g(x)在[-1,1]上为减函数,所以$B=[g(1),g(-1)]=[\frac{8}{3}+2m,\frac{8}{3}-2m]$;
由A⊆B得 $\left\{\begin{array}{l}\frac{8}{3}+2m≤-\frac{1}{3}\\ \frac{8}{3}-2m≥\frac{1}{3}\\ m≤-\sqrt{2}\end{array}\right.$,解得 $m≤-\frac{3}{2}$.
②当$m≥\sqrt{2}$时,函数g(x)在[-1,1]上为增函数,所以$B=[g(-1),g(1)]=[\frac{8}{3}-2m,\frac{8}{3}+2m]$,
由A⊆B得 $\left\{\begin{array}{l}\frac{8}{3}-2m≤-\frac{1}{3}\\ \frac{8}{3}+2m≥\frac{1}{3}\\ m≥\sqrt{2}\end{array}\right.$,解得$m≥\frac{3}{2}$.
综上可知,实数m的取值范围为$m≤-\frac{3}{2}$或$m≥\frac{3}{2}$.
点评 本题主要考查函数的单调性、奇偶性的应用,集合间的包含关系,体现了转化、分类讨论的数学思想,属于中档题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}$ | B. | $-\frac{i}{5}$ | C. | $\frac{2i}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
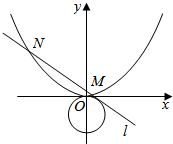 已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{{x}^{2}}$ | B. | (3x)′=3xlog3e | ||
| C. | (log23x)′=$\frac{1}{xln2}$ | D. | (x2cos x)′=-2xsin x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com