
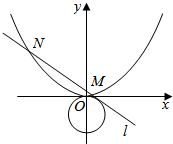
 已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).分析 (Ⅰ) 设抛物线方程为x2=2py,把点(2,1)代入运算求得 p的值,即可求得抛物线的标准方程;
(Ⅱ) 由直线与圆相切可得$\frac{{|{t+1}|}}{{\sqrt{1+{k^2}}}}=1⇒{k^2}={t^2}+2t$,把直线方程代入抛物线方程并整理,由△>0求得t的范围.利用根与系数的关系及∠MON为直角则$\overrightarrow{OM}•\overrightarrow{ON}=0$,求得t=4,运用弦长公式求得|MN|,求得点O到直线的距离,从而求得△OMN的面积.
解答  解:(Ⅰ) 设抛物线方程为x2=2py,
解:(Ⅰ) 设抛物线方程为x2=2py,
由已知得:22=2p所以p=2,
所以抛物线的标准方程为x2=4y;
(Ⅱ)因为直线与圆相切,
所以$\frac{{|{t+1}|}}{{\sqrt{1+{k^2}}}}=1⇒{k^2}={t^2}+2t$,
把直线方程代入抛物线方程并整理得:x2-4kx-4t=0,
由△=16k2+16t=16(t2+2t)+16t>0得 t>0或t<-3,
设M(x1,y1),N(x2,y2),
则x1+x2=4k且x1•x2=-4t,
${y_1}•{y_2}=(k{x_1}+t)•(k{x_2}+t)={k^2}{x_1}{x_2}+kt({x_1}+{x_2})+{t^2}={t^2}$
∵∠MON为直角∴$\overrightarrow{OM}•\overrightarrow{ON}=0$,解得t=4或t=0(舍去),
∵$|{MN}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=4\sqrt{(1+{k^2})({{t^2}+3t})}$,
点O到直线的距离为$\frac{|t|}{{\sqrt{1+{k^2}}}}$,
∴${S_{△mon}}=2\sqrt{{t^4}+3{t^3}}$=$16\sqrt{7}$.
点评 本题主要考查直线和圆的位置关系,向量的数量积公式的应用,点到直线的距离公式,考查化简整理的运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
 如图,在边长为2的正方体ABCD-A1B1C1D1中,P、Q分别为棱AB、A1D1的中点,M、N分别为面BCC1B1和DCC1D1上的点,一质点从点P射向点M,遇正方体的面反射(反射服从光的反射原理),反射到点N,再经平面反射,恰好反射至点Q,则三条线段PM、MN、NQ的长度之和为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,P、Q分别为棱AB、A1D1的中点,M、N分别为面BCC1B1和DCC1D1上的点,一质点从点P射向点M,遇正方体的面反射(反射服从光的反射原理),反射到点N,再经平面反射,恰好反射至点Q,则三条线段PM、MN、NQ的长度之和为( )| A. | $\sqrt{22}$ | B. | $\sqrt{21}$ | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
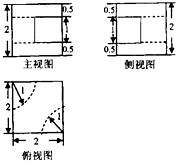
| A. | 8-$\frac{π}{6}$ | B. | 8-$\frac{π}{4}$ | C. | 8-$\frac{π}{3}$ | D. | 8-$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
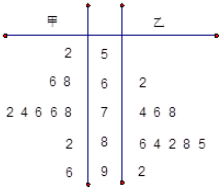
| A. | a1<a2,s1>s2 | B. | a1<a2,s1<s2 | C. | a1>a2,s1>s2 | D. | a1>a2,s1<s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com