Question

17．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x}+x-1（x＜0）}\\{-\frac{1}{3}{x}^{3}+2x（x≥0）}\end{array}\right.$，给出如下四个命题：
①f（x）在[$\sqrt{2}$，+∞）上是减函数；
②f（x）≤$\frac{\sqrt{2}}{3}$在R上恒成立；
③函数y=f（x）图象与直线y=-$\sqrt{3}$有两个交点．
其中真命题的个数为（　　）

• A． 3个
• B． 2个
• C． 1个
• D． 0个

Answer 1

分析 ①x∈[$\sqrt{2}$，+∞），f（x）=$-\frac{1}{3}{x}^{3}$+2x，f′（x）=-x²+2=-$（x+\sqrt{2}）（x-\sqrt{2}）$，由f′（x）≤0，即可得出f（x）在[$\sqrt{2}$，+∞）上单调性；
②x＜0，函数f（x）=e^x+x-1单调递增，可得f（x）＜f（0）；利用导数研究其单调性可得：当x=$\sqrt{2}$时，函数f（x）取得极大值即最大值，$f（\sqrt{2}）$=$\frac{4\sqrt{2}}{3}$，即可判断出正误；
③由①②画出函数f（x）的图象，即可判断出正误．

解答 解：①x∈[$\sqrt{2}$，+∞），f（x）=$-\frac{1}{3}{x}^{3}$+2x，f′（x）=-x²+2=-$（x+\sqrt{2}）（x-\sqrt{2}）$，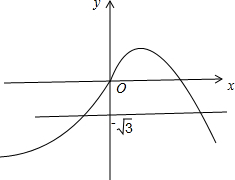
∵x∈[$\sqrt{2}$，+∞），∴f′（x）≤0，∴f（x）在[$\sqrt{2}$，+∞）上是减函数，正确；
②x＜0，函数f（x）=e^x+x-1单调递增，∴f（x）＜f（0）=1+0-1=0；当x≥$\sqrt{2}$时，由①可得：f′（x）≤0，函数f（x）
单调递减；当$0≤x＜\sqrt{2}$时，f′（x）＞0，函数f（x）单调递增．∴当x=$\sqrt{2}$时，函数f（x）取得极大值即最大值，
$f（\sqrt{2}）$=$-\frac{1}{3}×（\sqrt{2}）^{3}$+2$\sqrt{2}$=$\frac{4\sqrt{2}}{3}$，因此②不正确．
③由①②画出函数f（x）的图象，可得：函数y=f（x）图象与直线y=-$\sqrt{3}$有两个交点，正确．
综上可得：真命题的个数是2．
故选：B．

点评 本题考查了分段函数的性质、利用导数研究函数的单调性极值与最值，考查了数形结合的思想方法、推理能力与计算能力，属于难题．