
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
分析 利用对数函数的单调性求解.
解答 解:∵a=$\frac{1}{3}$ln$\frac{9}{4}$=ln$\root{3}{\frac{9}{4}}$,b=$\frac{4}{5}$ln$\frac{5}{4}$=ln$\root{5}{(\frac{5}{4})^{4}}$,c=$\frac{1}{4}$ln4=ln$\root{4}{4}$=ln$\sqrt{2}$,
y=lnx是增函数,$\root{5}{(\frac{5}{4})^{4}}$<$\root{3}{\frac{9}{4}}$<$\sqrt{2}$,
∴b<a<c.
故选:B.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意对数函数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 99 | B. | 100 | C. | 198 | D. | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α∥β,a?α,则a∥β | B. | 若a?α,b?β,α⊥β,则a⊥b | ||
| C. | 若a∥α,a∥b,则b∥α | D. | 若a∥α,b∥α,则a∥b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
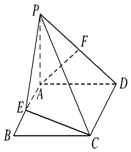 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点,∠ADP=45°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com