Question

8．定义在实数集R上的函数f（x），满足f（x）=f（2-x）=f（x-2），当x∈[0，1]时，f（x）=x•2^x．则函数g（x）=f（x）-|lgx|的零点个数为（　　）

• A． 99
• B． 100
• C． 198
• D． 200

Answer 1

分析 判断f（x）的对称性和周期，做出y=f（x）和y=|lgx|的函数图象，根据两图象的变化规律判断交点个数，从而得出结论．

解答 解：∵f（x）=f（x-2），∴f（x）是以2为周期的函数，
又f（2-x）=f（x-2），∴f（x）是偶函数，
∵f（x）=f（2-x），∴f（x）的图象关于直线x=1对称，
令g（x）=0得f（x）=|lgx|，
做出y=f（x）和y=|lgx|的函数图象如图所示：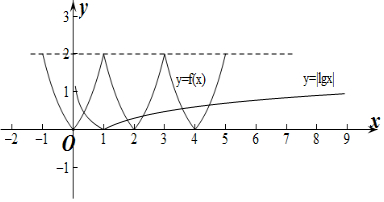

令lgx=2得x=100，
由图象可得y=f（x）和y=|lgx|的函数图象在每个区间[n-1，n]上都有1个交点，n=1，2，3，…，100．
∴g（x）共有100个零点．
故选B．

点评 本题考查了函数零点个数与函数图象的关系，函数周期性，对称性的应用，属于中档题．