
已知A,B,C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆的中心O,且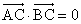 ,
,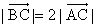 ,
,
(1)求椭圆的方程;
(2)如果椭圆上的两点P,Q使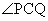 的平分线垂直于OA,是否总存在实数
的平分线垂直于OA,是否总存在实数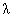 ,使得
,使得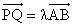 ?请说明理由;
?请说明理由;
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
提高过江大桥的车辆通行能力可改善整个城市的交通状况. 在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数. 当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明; 当
当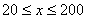 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(Ⅰ)当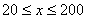 时,求函数
时,求函数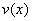 的表达式;
的表达式;
(Ⅱ)当车流密度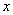 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知各项均为正数的数列{an}满足:a1=3,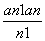 =
=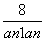 (n∈N*),设bn=
(n∈N*),设bn=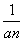 ,Sn=b
,Sn=b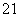 +b
+b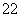 +…+b
+…+b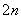 .
.
(1)求数列{an}的通项公式;
(2)求证:Sn< .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图13所示,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高度是46 m,则河流的宽度BC约等于________m.(用四舍五入法将结果精确到个位.参考数据:sin 67°≈0.92,cos 67°≈0.39,sin 37°≈0.60,cos 37°≈0.80,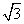 ≈1.73)
≈1.73)
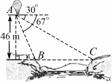 图13
图13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com