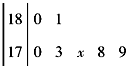练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知记录7名运动员选手身高（单位：cm）的茎叶图如图，其平均身高为177cm，因有一名运动员的身高记录看不清楚，设其末位数为x，那么推断x的值为（　　）
    A．5B．6C．7D．8

    分析 利用茎叶图的性质求解．

    解答 解：∵记录7名运动员选手身高（单位：cm）的茎叶图如图，
    其平均身高为177cm，
    ∴$\frac{1}{7}（180+181+170+173+170+x+178+179）$=177，
    解得x=8．
    故选：D．

    点评 本题考查茎叶图中的未知数的求法，是基础题，解题时要认真审题，注意茎叶图的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．已知{an}为等差数列，若a1+a5+a9=5π，则sin（a2+a8）的值为（　　）
    A．-$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．$\frac{1}{2}$D．-$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知数列{an}满足an+1=1-$\frac{1}{a_n}$（n∈N*），且a1=2，则a2017=（　　）
    A．-1B．$\frac{1}{2}$C．$\frac{3}{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．解一元二次方程ax2+bx+c=0（a≠0）利用求根公式解的集合为{$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$}或{-$\frac{b}{2a}$}或∅．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设命题p：?n0∈N，n02＞2n0，则￢p为（　　）
    A．?n∉N，n2≤2nB．$?{n_0}∈N，{n_0}^2≤{2^{n_0}}$
    C．?n∈N，n2≤2nD．$?{n_0}∉N，{n_0}^2≤{2^{n_0}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．在等比数列{an}中，若an＞0，a8=$\sqrt{2}$，则a5+a11有最小值是2$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．有5张卡片上分别写有数字1，2，3，4，5从这5张卡片中随机抽取2张，那么取出的2张卡片上的数字之积为偶数的概率为（　　）
    A．$\frac{1}{3}$B．$\frac{2}{3}$C．$\frac{7}{10}$D．$\frac{3}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设平面α∥平面β，直线a?α，点B∈β，则在β内过点B的所有直线中（　　）
    A．不存在与a平行的直线B．存在唯一一条与a平行的直线
    C．存在无数条与a平行的直线D．只有两条与a平行的直线

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．过点M（0，-3）的直线l与以点A（3，0），B（-4，1）为端点的线段AB有公共点，则直线l的斜率k的取值范围为（　　）
    A．[-1，1]B．（-∞，-1]∪[1，+∞）C．（-∞，-1）∪（1，+∞）D．（-1，1）

    查看答案和解析>>

    同步练习册答案