
分析 利用一元二次方程的求根公式和列举法写出集合即可.
解答 解:①当△=b2-4ac>0时,一元二次方程ax2+bx+c=0(a≠0)的解为:x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$;
②当△=b2-4ac=0时,一元二次方程ax2+bx+c=0(a≠0)的解为:x=-$\frac{b}{2a}$;
③当△=b2-4ac<0时,一元二次方程ax2+bx+c=0(a≠0)无解.
综上所述,符合条件的集合是:{$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$}或{-$\frac{b}{2a}$}或∅.
故答案是:{$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$}或{-$\frac{b}{2a}$}或∅.
点评 本题考查了集合的表示方法--列举法:常用于表示有限集合,把集合中的所有元素一一列举出来,写在大括号内,这种表示集合的方法叫做列举法.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | f(3)<f(-2)<f(1) | B. | f(1)<f(-2)<f(3) | C. | f(1)<f(3)<f(-2) | D. | f(-2)<f(3)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
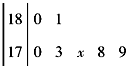 已知记录7名运动员选手身高(单位:cm)的茎叶图如图,其平均身高为177cm,因有一名运动员的身高记录看不清楚,设其末位数为x,那么推断x的值为( )
已知记录7名运动员选手身高(单位:cm)的茎叶图如图,其平均身高为177cm,因有一名运动员的身高记录看不清楚,设其末位数为x,那么推断x的值为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-2x+1 | B. | f(x)=-x2 | C. | f(x)=-$\frac{1}{x}$ | D. | f(x)=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com