
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点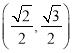 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点
的右顶点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】试题分析:(1)由双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() :
: ![]() (
(![]() )的顶点可得
)的顶点可得![]() 再由椭圆
再由椭圆![]() 经过点
经过点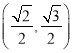 可得
可得 ![]() ,从而可得求椭圆
,从而可得求椭圆![]() 的方程;(2)设直线
的方程;(2)设直线![]() :
: ![]() ,联立
,联立![]() :
: ![]() ,得
,得![]() ,根据韦达定理及三角形面积公式将当
,根据韦达定理及三角形面积公式将当![]() 的面积用
的面积用![]() 表示,利用基本不等式等号成立的条件,可得当
表示,利用基本不等式等号成立的条件,可得当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
试题解析:(1)由已知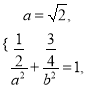 得
得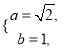
所以![]() 的方程为
的方程为![]() .
.
(2)由已知结合(1)得, ![]() ,
, ![]() ,
,
所以设直线![]() :
: ![]() ,联立
,联立![]() :
: ![]() ,得
,得![]() ,
,
得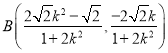 ,
,
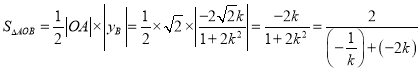 (
(![]() ),
),
当且仅当![]() ,即
,即![]() 时,
时, ![]() 的面积取得最大值,
的面积取得最大值,
所以![]() ,此时
,此时![]() ,
,
所以直线![]() :
: ![]() ,联立
,联立![]() ,解得
,解得![]() ,
,
所以![]() ,点
,点![]() 到直线
到直线![]() :
: ![]() 的距离为
的距离为![]() ,
,
所以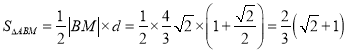 .
.
【方法点晴】本题主要考查待定系数法求椭圆方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形最值的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】四棱锥PABCD的三视图如图所示,四棱锥PABCD的五个顶点都在一个球面上, E,F分别是棱AB,CD的中点,直线EF被球面所截得的线段长为2![]() ,则该球的表面积为
,则该球的表面积为
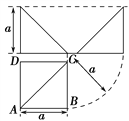
A. 12π B. 24π C. 36π D. 48π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856306)
在△ABC中,内角A,B,C的对边分别为a,b,c,已知![]() ,且b=5,acos C=-1.
,且b=5,acos C=-1.
(Ⅰ)求角A;
(Ⅱ)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856334)
已知函数f(x)=ln x+ax2+1.
(Ⅰ)当a=-1时,求函数f(x)的极值;
(Ⅱ)当a>0时,证明:存在正实数λ,使得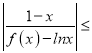 λ恒成立.
λ恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线C:
为抛物线C:![]() 的焦点,过点
的焦点,过点![]() 的动直线
的动直线![]() 与抛物线C交于
与抛物线C交于![]() ,
,![]() 两点,如图.当直线
两点,如图.当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() .
.
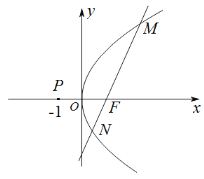
(1)求抛物线C的方程;
(2)已知点![]() ,设直线PM的斜率为
,设直线PM的斜率为![]() ,直线PN的斜率为
,直线PN的斜率为![]() .请判断
.请判断![]() 是否为定值,若是,写出这个定值,并证明你的结论;若不是,说明理由.
是否为定值,若是,写出这个定值,并证明你的结论;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即时间t(h)内沙尘暴所经过的路程s(km).

(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x>0时, ![]() .给出以下命题:
.给出以下命题:
①当x<0时,f(x)=ex(x+1);
②函数f(x)有五个零点;
③若关于x的方程f(x)=m有解,则实数m的取值范围是f(-2)≤m≤f(2);
④对x1,x2∈R,|f(x2)-f(x1)|<2恒成立.
其中,正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 在区间
在区间![]() 上是单调函数,试求实数
上是单调函数,试求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,且
,且![]() ,若函数
,若函数![]() 在区间
在区间![]() 上恰有3个零点,求实数
上恰有3个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com