
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切正整数
,对一切正整数![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上,记
的图象上,记![]() 与
与![]() 的等差中项为
的等差中项为![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设集合![]() ,
,![]() ,等差数列
,等差数列![]() 的任意一项
的任意一项![]() ,其中
,其中![]() 是
是![]() 中的最小数,且
中的最小数,且![]() ,求
,求![]() 的通项公式.
的通项公式.
科目:高中数学 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() 则
则![]()
②若![]() 则
则![]()
③若![]() 则
则![]()
④若![]() 则
则![]()
其中正确命题的序号是( )
A.①和③B.②和③C.②和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且图象的两相邻对称轴间的距离为
,且图象的两相邻对称轴间的距离为![]() .
.
(1)求![]() 的值;
的值;
(2)求方程![]() 在
在![]() 上的解的集合;
上的解的集合;
(3)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,若
的图象,若![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱锥C-ADE的体积;
(II)求证:平面ACE⊥平面CDE;
(III)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]() 底面
底面![]() ,且
,且![]() ,设
,设![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
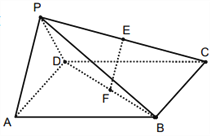
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着全民健康运动的普及,每天一万步已经成为一种健康时尚,某学校为了教职工健康工作,在全校范围内倡导“每天一万步”健步走活动,学校界定一人一天走路不足4千步为健步常人,不少于16千步为健步超人,其他为健步达人,学校随机抽查了36名教职工,其每天的走步情况统计如下:
步数 |
|
|
|
人数 | 6 | 18 | 12 |
现对抽查的36人采用分层抽样的方式选出6人
(1)求从这三类人中各抽多少人;
(2)现从选出的6人中随机抽取2人,求这两人健步类型相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com