
已知等比数列{an}的前n项和Sn=2n-a,n∈N*.设公差不为零的等差数列{bn}满足:b1=a1+2,且b2+5,b4+5,b8+5成等比数列.
(Ⅰ)求a的值及数列{bn}的通项公式;
(Ⅱ)设数列{log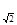 an}的前n项和为Tn.求使Tn>bn的最小正整数n.
an}的前n项和为Tn.求使Tn>bn的最小正整数n.
(Ⅰ)a=1,bn=8n-5;(Ⅱ)9.
解析试题分析:(Ⅰ)依据Sn=2n-a,根据数列的前n项和,求出数列{an}的通项公式,并且根据初始条件求出a=1,an=2n-1,再根据b2+5,b4+5,b8+5成等比数列,得出(b4+5)2=(b2+5)(b8+5),解得d=0(舍去),或d=8,从而求出{bn}的通项公式为bn=8n-5;(Ⅱ)由(Ⅰ)an=2n-1代入log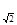 an=2(n-1),易知该数列是等差数列,根据等差数列的前n项和,求出Tn=
an=2(n-1),易知该数列是等差数列,根据等差数列的前n项和,求出Tn=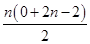 =n(n-1),而bn=8n-5,根据Tn>bn,n(n-1)>8n-5,解得n≥9,故所求n的最小正整数为9.
=n(n-1),而bn=8n-5,根据Tn>bn,n(n-1)>8n-5,解得n≥9,故所求n的最小正整数为9.
试题解析:
(Ⅰ)当n=1时,a1=S1=2-a;
当n≥2时,an=Sn-Sn-1=2n-1.
∵{an}为等比数列,
∴2-a=1,解得a=1.
∴an=2n-1.
设数列{bn}的公差为d,
∵b2+5,b4+5,b8+5成等比数列,
∴(b4+5)2=(b2+5)(b8+5),
又b1=3,
∴(8+3d)2=(8+d)(8+7d),
解得d=0(舍去),或d=8.
∴bn=8n-5.
(Ⅱ)由an=2n-1,得log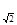 an=2(n-1),
an=2(n-1),
∴{log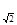 an}是以0为首项,2为公差的等差数列,
an}是以0为首项,2为公差的等差数列,
∴Tn=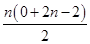 =n(n-1).
=n(n-1).
由bn=8n-5,Tn>bn,得
n(n-1)>8n-5,即n2-9n+5>0,
∵n∈N*,∴n≥9.
故所求n的最小正整数为9.
考点:1.数列通项公式的求解;2.等差、等比数列的性质应用.


科目:高中数学 来源: 题型:解答题
已知数列 的首项
的首项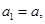 其中
其中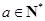 ,
,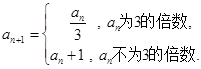 令集合
令集合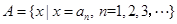 .
.
(Ⅰ)若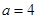 ,写出集合
,写出集合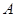 中的所有的元素;
中的所有的元素;
(Ⅱ)若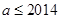 ,且数列
,且数列 中恰好存在连续的7项构成等比数列,求
中恰好存在连续的7项构成等比数列,求 的所有可能取值构成的集合;
的所有可能取值构成的集合;
(Ⅲ)求证: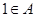 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业为扩大生产规模,今年年初新购置了一条高性能的生产线,该生产线在使用过程中的设备维修、燃料和动力等消耗的费用(称为设备的低劣化值)会逐年增加,第一年设备低劣化值是4万元,从第二年到第七年,每年设备低劣化值均比上年增加2万元,从第八年开始,每年设备低劣化值比上年增加25%.
(1)设第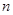 年该生产线设备低劣化值为
年该生产线设备低劣化值为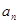 ,求
,求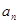 的表达式;
的表达式;
(2)若该生产线前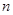 年设备低劣化平均值为
年设备低劣化平均值为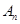 ,当
,当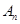 达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
达到或超过12万元时,则当年需要更新生产线,试判断第几年需要更新该生产线,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com