
(本题满分14分)本题有2个小题,第一小题满分6分,第二小题满分1分.
设常数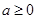 ,函数
,函数
(1)若 =4,求函数
=4,求函数 的反函数
的反函数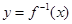 ;
;
(2)根据 的不同取值,讨论函数
的不同取值,讨论函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
(1)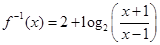 ,
,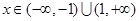 ;(2)
;(2)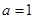 时
时 为奇函数,当
为奇函数,当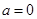 时
时 为偶函数,当
为偶函数,当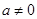 且
且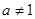 时
时 为非奇非偶函数.
为非奇非偶函数.
解析试题分析:(1)求反函数,就是把函数式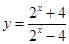 作为关于
作为关于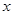 的方程,解出
的方程,解出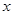 ,得
,得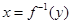 ,再把此式中的
,再把此式中的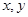 互换,即得反函数的解析式,还要注意的是一般要求出原函数的值域,即为反函数的定义域;(2)讨论函数的奇偶性,我们可以根据奇偶性的定义求解,在
互换,即得反函数的解析式,还要注意的是一般要求出原函数的值域,即为反函数的定义域;(2)讨论函数的奇偶性,我们可以根据奇偶性的定义求解,在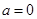 ,
,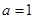 这两种情况下,由奇偶性的定义可知函数
这两种情况下,由奇偶性的定义可知函数 具有奇偶性,在
具有奇偶性,在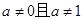 时,函数的定义域是
时,函数的定义域是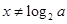 ,不关于原点对称,因此函数既不是奇函数也不是偶函数.
,不关于原点对称,因此函数既不是奇函数也不是偶函数.
试题解析:(1)由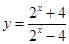 ,解得
,解得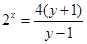 ,从而
,从而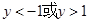 ,
,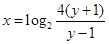
∴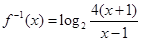 ,
,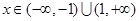
∵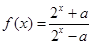 且
且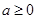
∴①当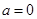 时,
时,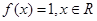 ,
,
∴对任意的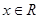 都有
都有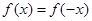 ,∴
,∴ 为偶函数
为偶函数
②当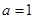 时,
时,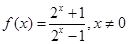 ,
,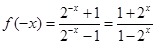 ,
,
∴对任意的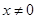 且
且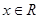 都有
都有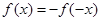 ,∴
,∴ 为奇函数
为奇函数
③当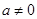 且
且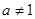 时,定义域为
时,定义域为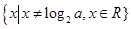 ,
,
∴定义域不关于原定对称,∴ 为非奇非偶函数
为非奇非偶函数
【考点】反函数,函数奇偶性.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=-x2+2ex+m-1,g(x)=x+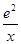 (x>0).
(x>0).
(1)若g(x)=m有实数根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义域为R的函数f(x)为奇函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
(1)求f(x)在[-1,0)上的解析式;
(2)求f(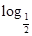 24)的值.
24)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程f(x)= 在(0,1]上解的个数.
在(0,1]上解的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com