
【题目】在平面直角坐标系![]() 中,已知动点
中,已知动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 为定直线
为定直线![]() 上一点.
上一点.
①过点![]() 作
作![]() 的垂线交轨迹
的垂线交轨迹![]() 于点
于点![]() (
(![]() 不在
不在![]() 轴上),求证:直线
轴上),求证:直线![]() 与
与![]() 的斜率之积是定值;
的斜率之积是定值;
②若点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作动直线
作动直线![]() 交轨迹
交轨迹![]() 于不同两点
于不同两点![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,求证:点
,求证:点![]() 恒在一条定直线上.
恒在一条定直线上.
【答案】(1)![]() (2)①直线
(2)①直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
②点![]() 在定直线
在定直线![]() 上.
上.
【解析】试题分析:(1)设动点坐标![]() ,直接利用轨迹方程定义计算即可;(2)
,直接利用轨迹方程定义计算即可;(2)![]() ,
,
①令![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,即
,即![]() ,又因为点
,又因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,而
,而![]() 的斜率分别为
的斜率分别为![]() ,于是
,于是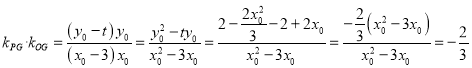 ,即直线
,即直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ; ②令
; ②令![]() ,则
,则![]() ,代入椭圆,消元即可证明点
,代入椭圆,消元即可证明点![]() 在定直线
在定直线![]() 上.
上.
试题解析:(1)设![]() ,则
,则![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
由![]() ,得
,得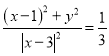 ,化简得
,化简得![]() ,
,
即点![]() 在轨迹
在轨迹![]() 的方程为
的方程为![]() ;
;
(2)因为![]() 为直线
为直线![]() 上一点,所以令
上一点,所以令![]() ,
,
①令![]() ,由
,由![]() ,得
,得![]() ,即
,即![]() ,即
,即![]() ,
,
又因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
而![]() 的斜率分别为
的斜率分别为![]() ,
,
于是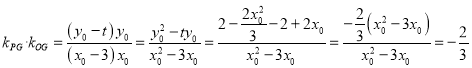 ,
,
即直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]()
.
②令![]() ,则
,则![]() ,
,
令点![]() ,则
,则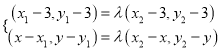 ,
,
即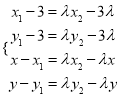 ,即
,即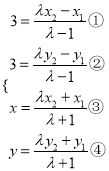
由①×③,②×④,得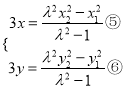 ,
,
因为![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
⑤×2+⑥×3,得![]()
![]() ,即
,即![]() ,
,
所以点![]() 在定直线
在定直线![]() 上.
上.
本题主要考查了椭圆的方程及直线与椭圆的位置关系,是高考的必考点,属于难题.求椭圆方程的方法一般就是根据条件建立![]() 的方程,求出
的方程,求出![]() 即可,注意
即可,注意![]() 的应用;涉及直线与圆锥曲线相交时,未给出直线时需要自己根据题目条件设直线方程,要特别注意直线斜率是否存在的问题,避免不分类讨论造成遗漏,然后要联立方程组,得一元二次方程,利用根与系数关系写出
的应用;涉及直线与圆锥曲线相交时,未给出直线时需要自己根据题目条件设直线方程,要特别注意直线斜率是否存在的问题,避免不分类讨论造成遗漏,然后要联立方程组,得一元二次方程,利用根与系数关系写出![]() ,再根据具体问题应用上式,其中要注意判别式条件的约束作用.
,再根据具体问题应用上式,其中要注意判别式条件的约束作用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】有甲、乙两个粮食经销商每次在同一粮食生产地以相同的价格购进粮食,他们共购进粮食两次,各次的粮食价格不同,甲每次购粮10000千克,乙每次购粮食10000元,在两次统计中,购粮的平均价格较低的是( )
A.甲
B.乙
C.一样低
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 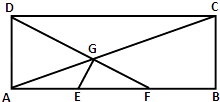
(1)若动点M到D点距离等于它到C点距离的两倍,求动点M的轨迹围成区域的面积;
(2)证明:E G⊥D F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
(Ⅰ) 证明:BM⊥平面AEC;
(Ⅱ) 求MC与平面DEC所成的角的余弦值.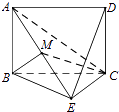
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知a3=24,S11=0.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}的前n项和Sn;
(Ⅲ)当n为何值时,Sn最大,并求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙、丙三个乒乓球协会的分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为A1 , A2 , A3 , 乙协会编号为A4 , 丙协会编号分别为A5 , A6 , 若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com