
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)函数![]() 是
是![]() 上的减函数 ;(2)见解析.
上的减函数 ;(2)见解析.
【解析】
(1)求出函数f(x)的定义域,并对函数f(x)求导,确定f′(x)的正负,即可确定函数f(x)在定义域上的单调性;(2)设a>b>0,分为两个不等式![]() 和
和![]() .证明不等式
.证明不等式![]() 时,转化为
时,转化为![]() ,换元t=
,换元t=![]() >1,转化为
>1,转化为![]() ,通过函数f(x)在区间(1,+∞)上的单调性来证明;证明不等式
,通过函数f(x)在区间(1,+∞)上的单调性来证明;证明不等式![]() ,转化为
,转化为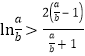 ,换元x=
,换元x=![]() >1,构造函数
>1,构造函数![]() ,通过函数g(x)在区间(1,+∞)的单调性来证明.
,通过函数g(x)在区间(1,+∞)的单调性来证明.
(1)函数f(x)的定义域为(0,+∞),![]() ,所以,函数f(x)在定义域(0,+∞)上单调递减;
,所以,函数f(x)在定义域(0,+∞)上单调递减;
(2)假设a>b>0.先证明不等式![]() ,即证
,即证![]() ,即证
,即证![]() ,令
,令![]() ,则原不等式即为
,则原不等式即为![]() ,其中t>1,由(1)知,函数f(x)在(0,+∞)上单调递减,当t>1时,f(t)<f(1)=0,即
,其中t>1,由(1)知,函数f(x)在(0,+∞)上单调递减,当t>1时,f(t)<f(1)=0,即
![]() ,即
,即![]() ,所以,当a>b>0时,
,所以,当a>b>0时,![]() .
.
下面证明![]() .即证
.即证![]() ,即
,即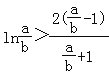 ,
,
令![]() ,即证
,即证![]() ,其中x>1,构造函数
,其中x>1,构造函数![]() ,其中x>1,
,其中x>1,![]() ,所以,函数g(x)在区间(1,+∞)上单调递增,所以,g(x)>g(1)=0,所以,当x>1时,
,所以,函数g(x)在区间(1,+∞)上单调递增,所以,g(x)>g(1)=0,所以,当x>1时,![]() ,
,
所以,当a>b>0时,![]() .
.
综上所述,当a>0,b>0时,![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() ,不过原点O的直线
,不过原点O的直线![]() 与C交于A,B两点,且线段AB被直线OP平分.
与C交于A,B两点,且线段AB被直线OP平分.
(1)求椭圆C的方程;
(2)求k的值;
(3)求![]() 面积取最大值时直线l的方程.
面积取最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中学生研学旅行是通过集体旅行、集中食宿方式开展的研究性学习和旅行体验相结合的校外教育活动,是学校教育和校外教育衔接的创新形式,是综合实践育人的有效途径.每年暑期都会有大量中学生参加研学旅行活动.为了解某地区中学生暑期研学旅行支出情况,在该地区各个中学随机抽取了部分中学生进行问卷调查,从中统计得到中学生暑期研学旅行支出(单位:百元)频率分布直方图如图所示.

(1)利用分层抽样在![]() ,
,![]() ,
,![]() 三组中抽取5人,应从这三组中各抽取几人?
三组中抽取5人,应从这三组中各抽取几人?
(2)从(1)抽取的5人中随机选出2人,对其消费情况进行进一步分析,求这2人不在同一组的概率;
(3)假设同组中的每个数据都用该区间的左端点值代替,估计该地区中学生暑期研学旅行支出的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 和
和![]() .
.
(![]() )若
)若![]() ,
, ![]() 是正方形一条边上的两个顶点,求这个正方形过顶点
是正方形一条边上的两个顶点,求这个正方形过顶点![]() 的两条边所在直线的方程;
的两条边所在直线的方程;
(![]() )若
)若![]() ,
, ![]() 是正方形一条对角线上的两个顶点,求这个正方形另外一条对角线所在直线的方程及其端点的坐标.
是正方形一条对角线上的两个顶点,求这个正方形另外一条对角线所在直线的方程及其端点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com