
����Ŀ����ѧ����ѧ������ͨ���������С�����ʳ��ʽ��չ���о���ѧϰ�������������ϵ�У����������ѧУ������У������νӵĴ�����ʽ�����ۺ�ʵ�����˵���Ч;��.ÿ�����ڶ����д�����ѧ���μ���ѧ���л.Ϊ�˽�ij������ѧ��������ѧ����֧��������ڸõ���������ѧ�����ȡ�˲�����ѧ�������ʾ����飬����ͳ�Ƶõ���ѧ��������ѧ����֧������λ����Ԫ��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.

��1�����÷ֲ������![]() ��
��![]() ��
��![]() �����г�ȡ5�ˣ�Ӧ���������и���ȡ���ˣ�
�����г�ȡ5�ˣ�Ӧ���������и���ȡ���ˣ�
��2���ӣ�1����ȡ��5�������ѡ��2�ˣ���������������н�һ������������2�˲���ͬһ��ĸ��ʣ�
��3������ͬ���е�ÿ�����ݶ��ø��������˵�ֵ���棬���Ƹõ�����ѧ��������ѧ����֧����ƽ��ֵ.
���𰸡���1�����������г�ȡ�������ֱ�Ϊ3��1��1��2��![]() ��3��
��3��![]() ��Ԫ
��Ԫ
��������
��1�����÷ֲ������Ƶ�ʷֲ�ֱ��ͼ������ٸ�����ı����������������
��2������������¼����������������2�˲���ͬһ��Ļ����¼�����������ʼ��ɣ�
��3����Ƶ�ʷֲ�ֱ��ͼ�����ʺ�ƽ�����ļ��㹫ʽ�������.
��1����Ƶ�ʷֲ�ֱ��ͼ��֪![]() ��
��![]() ��
��![]() �����Ƶ���ı�Ϊ
�����Ƶ���ı�Ϊ
![]() ��
��
���Դ�![]() �г�ȡ��
�г�ȡ��![]() �ˣ�
�ˣ�
��![]() �г�ȡ��
�г�ȡ��![]() �ˣ�
�ˣ�
��![]() �г�ȡ��
�г�ȡ��![]() �ˣ�
�ˣ�
���Դ��������г�ȡ�������ֱ�Ϊ3��1��1��
��2����![]() �е�3��Ϊ
�е�3��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �е�1��Ϊb��
�е�1��Ϊb��![]() �е�1��Ϊc��
�е�1��Ϊc��
����5�������ѡ��2�ˣ��������ռ�
![]() ��
��![]() �������㣬
�������㣬
���¼�A��ѡ����2�˲���ͬһ�飬
��![]() ��7�������㣬
��7�������㣬
����![]() ��
��
��3��![]() ��
��
���Ƹõ�����ѧ��������ѧ����֧����ƽ��ֵΪ![]() ��Ԫ.
��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[2019������һģ]��֪����![]() �У�
��![]() ��
��![]() ��������������ͼ��������е���ʱ�����������2�����жϿ��ڵ������������ǣ� ��
��������������ͼ��������е���ʱ�����������2�����жϿ��ڵ������������ǣ� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ǻ���
�Ǻ���![]() ����㣬
����㣬![]() .
.
��1����ʵ��![]() ��ֵ��
��ֵ��
��2��������ʽ![]() ��
��![]() �Ϻ��������ʵ��
�Ϻ��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3�������� ��������ͬ��ʵ���⣬��ʵ��
��������ͬ��ʵ���⣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����2![]() sin��3��x
sin��3��x![]() ������������0��
������������0��
��1����f��x+��������С����Ϊ2����ż����������������ֵ��
��2����f��x���ڣ�0��![]() ]���������������������ֵ��
]���������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��
��![]() ������������ʡ�人�г�����չ���м���ؼ�����⣬���ֶ����Է��ײ����������Ϊ�����Է��β���Ⱦ��������Ϊ����״�������ף�CoronaVirusDisease2019��COVID-19������ơ��¹ڷ��ס�����ͼ��
������������ʡ�人�г�����չ���м���ؼ�����⣬���ֶ����Է��ײ����������Ϊ�����Է��β���Ⱦ��������Ϊ����״�������ף�CoronaVirusDisease2019��COVID-19������ơ��¹ڷ��ס�����ͼ��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ���ۼ�ȷ��������ʱ��仯��ɢ��ͼ��
���ۼ�ȷ��������ʱ��仯��ɢ��ͼ��

Ϊ��Ԥ����δ��ȡǿ����ʩ�£����ڵ��ۼ�ȷ���������������ۼ�ȷ������![]() ��ʱ�����
��ʱ�����![]() �������ع�ģ�ͣ�����
�������ع�ģ�ͣ�����![]() ��
��![]() ����
����![]() ��
��![]() �յ����ݣ�ʱ�����
�յ����ݣ�ʱ�����![]() ��ֵ����
��ֵ����![]() ��
��![]() ������
������![]() ������ģ��
������ģ��![]() ��
��![]() ��
��
�ο����ݣ�����![]() ��
��![]() ��
��
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
��1������ɢ��ͼ�жϣ�![]() ��
��![]() ��һ��������Ϊ�ۼ�ȷ������
��һ��������Ϊ�ۼ�ȷ������![]() ��ʱ�����
��ʱ�����![]() �Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ���
�Ļع鷽�����ͣ��������жϼ��ɣ�����˵�����ɣ���
��2�����ݣ�1�����жϽ�������������ݣ�����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
��3��������![]() ��
��![]() ����
����![]() ��
��![]() ���ۼ�ȷ����������ʵ���ݣ����ݣ�2���Ľ���ش��������⣺
���ۼ�ȷ����������ʵ���ݣ����ݣ�2���Ľ���ش��������⣺
ʱ�� |
|
|
|
|
|
�ۼ�ȷ����������ʵ���� |
|
|
|
|
|
��i����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() �����ģ��Ԥ����������ʵ���ݲ�ֵ�ľ���ֵ����ʵ���ݵı�ֵ����С��
�����ģ��Ԥ����������ʵ���ݲ�ֵ�ľ���ֵ����ʵ���ݵı�ֵ����С��![]() ����Ϊģ�Ϳɿ������жϣ�2���Ļع鷽���Ƿ�ɿ���
����Ϊģ�Ϳɿ������жϣ�2���Ļع鷽���Ƿ�ɿ���
��ii��![]() ��
��![]() ��
��![]() ��������������ǿ���쵼�£�ȫ������ͬȡ��ǿ����Ԥ�����¹ڷ��ס��Ĵ�ʩ������ȡ��ʩ
��������������ǿ���쵼�£�ȫ������ͬȡ��ǿ����Ԥ�����¹ڷ��ס��Ĵ�ʩ������ȡ��ʩ![]() �����ʵ�������Ե���Ԥ�����ݣ�����Ϊ������ʩ��Ч�����ж�Ԥ����ʩ�Ƿ���Ч����˵������.
�����ʵ�������Ե���Ԥ�����ݣ�����Ϊ������ʩ��Ч�����ж�Ԥ����ʩ�Ƿ���Ч����˵������.
��������һ������![]() ��
��![]() ��������
��������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ�� ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������![]() �У���֪
�У���֪![]() ��
��![]() ��
��
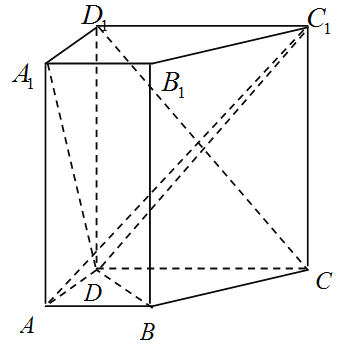
��1����֤��![]() ��
��
��2����![]() ��
��![]() ��һ�㣬��ȷ��
��һ�㣬��ȷ��![]() ��λ�ã�ʹ
��λ�ã�ʹ![]() ƽ��
ƽ��![]() ����˵�����ɣ�
����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ�����Ϊ[0��1]���ĺ���f��x�������ͬʱ���������������ٶ������x��[0��1]������f��x����0����f ��1����1������x1��0��x2��0��x1+x2��1������f��x1+x2����f��x1��+f��x2����������ƺ���f��x��Ϊ���뺯����
��1���жϺ���g��x����2x��1��x��[0��1]���Ƿ�Ϊ���뺯����������֤����
��2��������f��x��Ϊ���뺯�����ٶ�����x0��[0��1]��ʹ��f��x0����[0��1]����f��f��x0������x0����֤f��x0����x0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ����
��Բ����![]() ��ĸ������ϣ��뾶����5���ҹ���
��ĸ������ϣ��뾶����5���ҹ���![]() ��
��
��1����Բ![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ��Բ
��Բ![]() ����A��B���㣬��
����A��B���㣬��![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com