
【题目】已知f(x)=2|x+1|﹣|x﹣1|.
(1)画出函数f(x)的图象;
(2)解不等式|f(x)|>1.
【答案】
(1)解:当x≥1时,f(x)=2(x+1)﹣(x﹣1)=x+3;
当﹣1<x<1时,f(x)=2(x+1)﹣(1﹣x)=3x+1;
当x≤﹣1时,f(x)=﹣2(x+1)+(x﹣1)=﹣x﹣3,
所以 
(2)解:根据图象可得|f(x)|=1时,x=﹣4或﹣1或 ![]() 或0,
或0,
所以|f(x)|>1的解集为 ![]() .
.

【解析】(1)确定分段函数,即可画出函数f(x)的图象;(2)根据图象可得|f(x)|=1时,x=﹣4或﹣1或 ![]() 或0,即可解不等式|f(x)|>1.
或0,即可解不等式|f(x)|>1.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x+y)=f(x)·f(y),且f(1)=![]() .
.
(1)当n∈N+,求f(n)的表达式;
(2)设an=nf(n),n∈N+,求证:a1+a2+…+an<2.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)利用f(x+y)=f(x)f(y)(x,y∈R)通过令x=n,y=1,说明{f(n)}是以f(1)=![]() 为首项,公比为
为首项,公比为![]() 的等比数列求出
的等比数列求出![]() ;(2)利用(1)求出an=nf(n)的表达式,利用错位相减法求出数列的前n项和,即可说明不等式成立.
;(2)利用(1)求出an=nf(n)的表达式,利用错位相减法求出数列的前n项和,即可说明不等式成立.
(1)解:f(n)=f[(n-1)+1]
=f(n-1)·f(1)=![]() f(n-1).
f(n-1).
∴当n≥2时,![]() =
=![]() .
.
又f(1)=![]() ,
,
∴数列{f(n)}是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
∴f(n)=f(1)·(![]() )n-1=(
)n-1=(![]() )n.
)n.
(2)证明:由(1)可知,
an=n·(![]() )n=n·
)n=n·![]() ,
,
设Sn=a1+a2+…+an,
则Sn=![]() +2×
+2×![]() +3×
+3×![]() +…+(n-1)·
+…+(n-1)·![]() +n·
+n·![]() ,①
,①
∴![]() Sn=
Sn=![]() +2×
+2×![]() +…+(n-2)·
+…+(n-2)·![]() +(n-1)·
+(n-1)·![]() +n·
+n·![]() .②
.②
①-②得,
![]() Sn=
Sn=![]() +
+![]() +
+![]() +…+
+…+![]() -n·
-n·![]()
=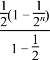 -
-![]() =1-
=1-![]() -
-![]() ,
,
∴Sn=2-![]() -
-![]() <2.
<2.
即a1+a2+…+an<2.
【点睛】
本题考查数列与函数的关系,数列通项公式的求法和的求法,考查不等式的证明,裂项法与错位相减法的应用,数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
【题型】解答题
【结束】
22
【题目】设数列{an}的前n项和为Sn.已知a1=a (a≠3),an+1=Sn+3n,n∈N+.
(1)设bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N+,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.

(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: ,).
,).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为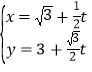 (t为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系.曲线C的极坐标方程为ρ=2
(t为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系.曲线C的极坐标方程为ρ=2![]() cosθ.
cosθ.
(1)求直线l的普通方程与曲线C的直角坐标方程。
(2)求出直线l与曲线C相交后的弦长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com