
如图,正方体ABCD-A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F.求证:EF∥平面ABCD.
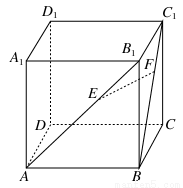
见解析
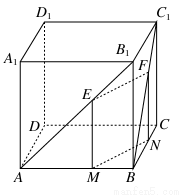
【解析】证明:方法一:过E作EM⊥AB于M,过F作FN⊥BC于N,连接MN,如图所示,则EM∥BB1,FN∥BB1,
∴EM∥FN.
∵AB1=BC1,B1E=C1F,
∴AE=BF,
∴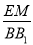 =
=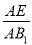 ,
,
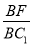 =
=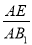 =
=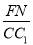 ,
,
∴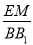 =
=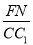 .
.
又∵BB1=CC1,∴EM=FN,
∴四边形EMNF是平行四边形,
∴EF∥MN.
又∵EF?平面ABCD,MN?平面ABCD,
∴EF∥平面ABCD.
方法二:过点E作EH⊥BB1于点H,连接FH,如图所示,则EH∥AB,所以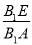 =
=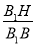 .
.
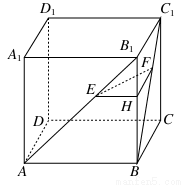
∵AB1=BC1,B1E=C1F,
∴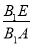 =
=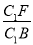 ,
,
∴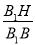 =
=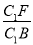 ,
,
∴FH∥B1C1.
∵B1C1∥BC,∴FH∥BC.
∵EH∩FH=H,
∴平面EFH∥平面ABCD.
∵EF?平面EFH,
∴EF∥平面ABCD.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-2直线的交点坐标与距离公式(解析版) 题型:填空题
已知直线l1:ax-y+2a=0,l2:(2a-1)x+ay+a=0互相垂直,则实数a的值是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-6空间向量及运算(解析版) 题型:解答题
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:
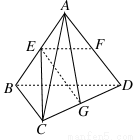
(1) ·
· ;
;
(2) ·
· ;
;
(3)EG的长;
(4)异面直线AG与CE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:填空题
设α、β、γ为彼此不重合的三个平面,l为直线,给出下列命题:
①若α∥β,α⊥γ,则β⊥γ;
②若α⊥γ,β⊥γ,且α∩β=l,则l⊥γ;
③若直线l与平面α内的无数条直线垂直,则直线l与平面α垂直;
④若α内存在不共线的三点到β的距离相等,则平面α平行于平面β;
上面命题中,真命题的序号为________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:选择题
已知α,β表示两个不同的平面,m为平面α内的一条直线,则“α⊥β”是“m⊥β”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-4直线、平面平行的判定及性质(解析版) 题型:选择题
如图中四个正方体图形,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是( )
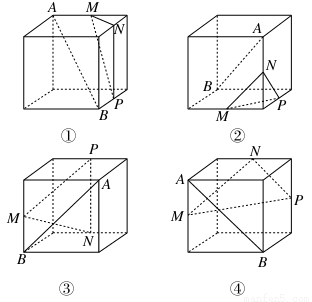
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-3空间点直线平面之间的位置关系(解析版) 题型:选择题
如图是正方体的展开图,则在这个正方体中:
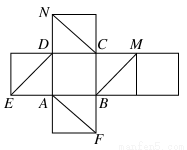
①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
A.①②③ B.②④ C.③④ D.②③④
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:解答题
一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点)
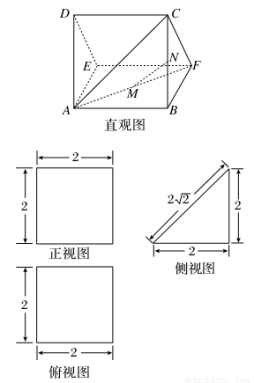
(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:选择题
已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )
A.(7,5) B.(5,7) C.(2,10) D.(10,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com