
如图,已知焦点在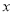 轴上的椭圆
轴上的椭圆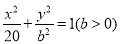 经过点
经过点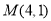 ,直线
,直线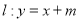
交椭圆于 不同的两点.
不同的两点.

(1)求该椭圆的标准方程;
(2)求实数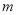 的取值范围;
的取值范围;
(3)是否存在实数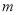 ,使△
,使△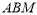 是以
是以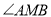 为直角的直角三角形,若存在,求出
为直角的直角三角形,若存在,求出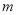 的值,若不存,请说明理由.
的值,若不存,请说明理由.
(1) (2)
(2) (3)见解析
(3)见解析
【解析】
试题分析:(1)设出椭圆方程的标准形式,由离心率的值及椭圆过点(4,1)求出待定系数,得到椭圆的标准方程.
(2)把直线方程代入椭圆的方程,由判别式大于0,求出m的范围即可;
(3)对于存在性问题,可先假设存在,即假设存在实数m满足题意,再利用△ABM为直角三角形,结合向量垂直的条件求出m,若出现矛盾,则说明假设不成立,即不存在;否则存在.
试题解析:【解析】
(1)依题意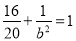 ,解得
,解得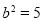 , 2分
, 2分
所以椭圆的标准方程是 . 3分
. 3分
(2)由 得
得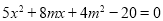 , 4分
, 4分
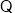 直线
直线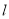 与椭圆有两个不同的交点,
与椭圆有两个不同的交点,
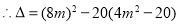
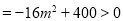 6分
6分
解得 7分
7分
(3)假设存在实数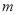 满足题意,则由
满足题意,则由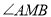 为直角得
为直角得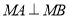 , 8分
, 8分
设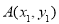 ,
, ,由(2)得
,由(2)得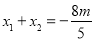 ,
, 9分
9分

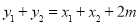 ,
,
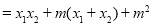 10分
10分
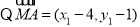 ,
, 11分
11分
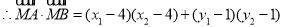
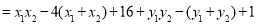
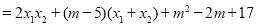 12分
12分
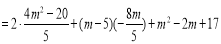
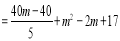
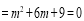 得
得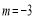 13分
13分
因为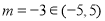 ,
,
综上所述,存在实数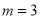 使△
使△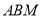 为直角三角形. 14分
为直角三角形. 14分
考点:1.直线与圆锥曲线的综合问题;2.椭圆的标准方程.


科目:高中数学 来源:2015届福建漳州实验中学高二(上)期末考试理科数学试卷(解析版) 题型:填空题
曲线C是平面内与两个定点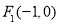 和
和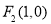 的距离的积等于常数
的距离的积等于常数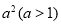 的点的轨迹,给出下列三个结论:
的点的轨迹,给出下列三个结论:
①曲线C过坐标原点; ②曲线C关于坐标原点对称;
③若点P在曲线C上,则△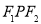 的面积不大于
的面积不大于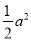 .
.
其中,所有正确结论的序号是____________.
查看答案和解析>>
科目:高中数学 来源:2015届福建漳州实验中学高二(上)期末考试理科数学试卷(解析版) 题型:选择题
设F1,F2分别是双曲线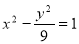 的左、右焦点.若点P在双曲线上,且
的左、右焦点.若点P在双曲线上,且 ·
· =0,则|
=0,则| +
+ |=( )
|=( )
A. B.
B.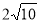 C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届福建漳州实验中学高二(上)期末考试文科数学试卷(解析版) 题型:填空题
为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com