
【题目】如图,在三棱柱![]() 中,
中, ![]() ,平面
,平面![]() 平面
平面![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,求
,求![]() .
.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)第(1)问,通过证明C1C⊥平面A1BC得到CC1⊥A1B. (2)第(2)问,以C为坐标原点,分别以![]() 的方向为x轴,y轴的正方向建立空间直角坐标系,利用空间向量求二面角A1-BC1-A的余弦值 .
的方向为x轴,y轴的正方向建立空间直角坐标系,利用空间向量求二面角A1-BC1-A的余弦值 .
试题解析:
(1)因为平面AA1C1C⊥平面ABC,交线为AC,又BC⊥AC,
所以BC⊥平面AA1C1C,
因为C1C![]() 平面AA1C1C,
平面AA1C1C,
从而有BC⊥C1C.
因为∠A1CC1=90°,所以A1C⊥C1C,
又因为BC∩A1C=C,
所以C1C⊥平面A1BC,
A1B![]() 平面A1BC,所以CC1⊥A1B.
平面A1BC,所以CC1⊥A1B.
(2)如图,以C为坐标原点,分别以![]() 的方向为x轴,y轴的正方向建立空间直角坐标系C-xyz.
的方向为x轴,y轴的正方向建立空间直角坐标系C-xyz.
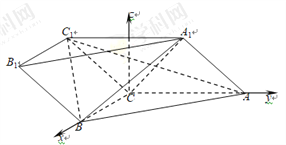
由∠A1CC1=90°,AC=![]() AA1得A1C=AA1.
AA1得A1C=AA1.
不妨设BC=AC=![]() AA1=2,
AA1=2,
则B(2,0,0),C1(0,-1,1),A(0,2,0),A1(0,1,1),
所以![]() =(0,-2,0),
=(0,-2,0), ![]() =(-2,-1,1),
=(-2,-1,1), ![]() =(2,-2,0),
=(2,-2,0),
设平面A1BC1的一个法向量为![]() ,
,
由![]() ·
·![]() =0,
=0, ![]() ·
·![]() =0,可取
=0,可取![]() =(1,0,2).
=(1,0,2).
设平面ABC1的一个法向量为![]() ,
,
由![]() ·
·![]() =0,
=0, ![]() ·
·![]() =0,可取
=0,可取![]() =(1,1,3).
=(1,1,3).
cos![]() ,
, ![]() =
=![]() =
=![]() ,
,
又因为二面角A1-BC1-A为锐二面角,
所以二面角A1-BC1-A的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为( )
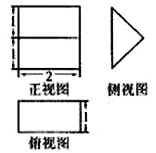
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】几何体如图,球心为O,半径为![]() ,表面积为
,表面积为![]() ,选B.
,选B.
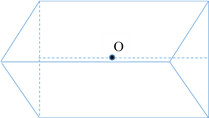
点睛:涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题转化为平面问题,再利用平面几何知识寻找几何体中元素间的关系,或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解.
【题型】单选题
【结束】
9
【题目】![]() 是双曲线
是双曲线![]() 的左右焦点,过
的左右焦点,过![]() 且斜率为1的直线与两条渐近线分别交于
且斜率为1的直线与两条渐近线分别交于![]() 两点,若
两点,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,其中
,其中![]() .函数
.函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为4.
与其相邻的最高点的距离为4.
(Ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)计算![]() 的值;
的值;
(Ⅲ)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间 [0,3] 上的零点个数.
在区间 [0,3] 上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】济南市某中学高三年级有1000名学生参加学情调研测试,用简单随机抽样的方法抽取了一个容量为50的样本,得到数学成绩的频率分布直方图如图所示.
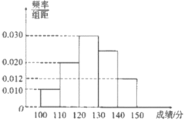
(1)求第四个小矩形的高,并估计本校在这次统测中数学成绩不低于120分的人数和这1000名学生的数学平均分;
(2)已知样本中,成绩在[140,150]内的有2名女生,现从成绩在这个分数段的学生中随机选取2人做学习交流,求选取的两人中至少有一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则存在唯一实数
,则存在唯一实数![]() ,使得
,使得![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,且
,且![]() 与
与![]() 的夹角为钝角,则
的夹角为钝角,则![]() ;⑤若平面内定点
;⑤若平面内定点![]() 满足
满足![]() ,则
,则![]() 为正三角形.其中正确的命题序号为 ________.
为正三角形.其中正确的命题序号为 ________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.

求证:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,且离心率为
,且离心率为![]() ,
, ![]() 为椭圆上任意一点,当
为椭圆上任意一点,当![]() 时,
时, ![]() 的面积为1.
的面积为1.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() 是椭圆
是椭圆![]() 上异于椭圆顶点的一点,延长直线
上异于椭圆顶点的一点,延长直线![]() ,
, ![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,
, ![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设![]() 由题
由题 ,由此求出
,由此求出![]() ,可得椭圆
,可得椭圆![]() 的方程;
的方程;
(2)设![]() ,
, ![]() ,
,
当直线![]() 的斜率不存在时,可得
的斜率不存在时,可得![]() ;
;
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,则由
,则由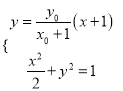 消去
消去![]() 通过运算可得
通过运算可得
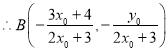 ,同理可得
,同理可得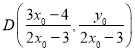 ,由此得到直线
,由此得到直线![]() 的斜率为
的斜率为![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,进而可得
,进而可得![]() .
.
试题解析:(1)设![]() 由题
由题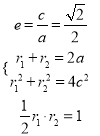 ,
,
解得![]() ,则
,则![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,
,
当直线![]() 的斜率不存在时,设
的斜率不存在时,设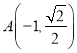 ,则
,则 ,
,
直线![]() 的方程为
的方程为![]() 代入
代入![]() ,可得
,可得![]() ,
,
![]() ,
, ![]() ,则
,则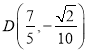 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为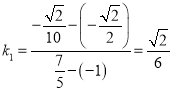 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
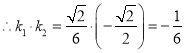 ,
,
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,则由
,则由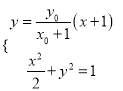 消去
消去![]() 可得:
可得:
![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得
,代入上述方程可得
![]() ,
,
![]() ,则
,则![]()
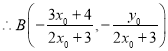 ,
,
设直线![]() 的方程为
的方程为![]() ,同理可得
,同理可得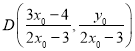 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为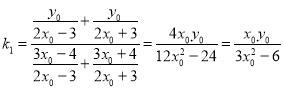 ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,
![]()
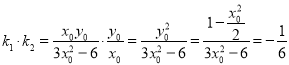 .
.
所以,直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若方程![]() 有两个实数根
有两个实数根![]() ,
, ![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设有一套住房的房价从2002年的20万元上涨到2012年的40万元,下表给出了两种价格增长方式,其中![]() 是按直线上升的房价,
是按直线上升的房价,![]() 是按指数增长的房价,t是2002年以来经过的年数.
是按指数增长的房价,t是2002年以来经过的年数.
t | 0 | 5 | 10 | 15 | 20 |
| 20 | 30 | 40 | 50 | 60 |
| 20 |
| 40 |
| 80 |
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的解析式;
的解析式;
(3)完成上表空格中的数据,并在同一直角坐标系中画出两个函数的图象,然后比较两种价格增长方式的差异.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
:![]() (
(![]() 为参数)和曲线
为参数)和曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)化![]() ,
,![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() ,
,![]() 为
为![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线![]() :
:![]() (
(![]() 为参数)距离的最小值及此时
为参数)距离的最小值及此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com