
分析 (Ⅰ)由条件利用两个向量的数量积公式、三角恒等变换化简函数的解析式为f(x)=5sin(2x+$\frac{π}{6}$)+5,再利用正弦函数的定义域和值域,求得函数f(x)的最小值.
(Ⅱ)当x∈[$\frac{π}{6}$,$\frac{π}{2}$]时,由f(x)=8求得 sin(2x+$\frac{π}{6}$)的值,可得cos(2x+$\frac{π}{6}$)的值,再根据f(x+$\frac{π}{8}$)=5sin[(2x+$\frac{π}{6}$)+$\frac{π}{4}$]+5,利用两角和的正弦公式计算求的结果.
解答 解:(Ⅰ)函数f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$+|$\overrightarrow{b}$|2+$\frac{3}{2}$=5$\sqrt{3}$sinxcosx+2cos2x+1+3cos2x+$\frac{3}{2}$
=5$\sqrt{3}$sinxcosx+5cos2x+$\frac{5}{2}$=$\frac{5\sqrt{3}}{2}$sin2x=5•$\frac{1+cos2x}{2}$+$\frac{5}{2}$=5sin(2x+$\frac{π}{6}$)+5,
当x∈[0,$\frac{π}{2}$]时,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
故当2x+$\frac{π}{6}$=$\frac{7π}{6}$,即x=$\frac{π}{2}$时,f(x)取得最小值为 $\frac{5}{2}$,
当2x+$\frac{π}{6}$=$\frac{π}{2}$,即x=$\frac{π}{6}$时,f(x)取得最大值为 10.
(Ⅱ)当x∈[$\frac{π}{6}$,$\frac{π}{2}$]时,∵f(x)=5sin(2x+$\frac{π}{6}$)+5=8,∴sin(2x+$\frac{π}{6}$)=$\frac{3}{5}$,∴cos(2x+$\frac{π}{6}$)=-$\frac{4}{5}$,
故f(x+$\frac{π}{8}$)=5sin(2x+$\frac{π}{4}$+$\frac{π}{6}$)+5=5sin[(2x+$\frac{π}{6}$)+$\frac{π}{4}$]+5=5sin(2x+$\frac{π}{6}$)cos$\frac{π}{4}$+5cos(2x+$\frac{π}{6}$)sin$\frac{π}{4}$+5
=5×$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$=5×(-$\frac{4}{5}$)×$\frac{\sqrt{2}}{2}$+5=5-$\frac{\sqrt{2}}{2}$.
点评 本题主要考查两个向量的数量积公式,三角恒等变换,正弦函数的定义域和值域,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
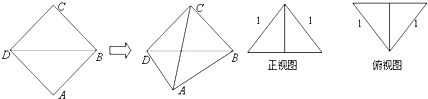
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
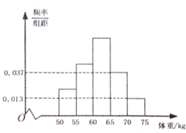 为了了解某校2015年高考准备报考“体育特长生”的学生体重情况,将所得数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前3个小组的频率之比为1:2:3,已知报考“体育特长生”的学生人数是48,则体重在[50,55)组的频数为( )
为了了解某校2015年高考准备报考“体育特长生”的学生体重情况,将所得数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前3个小组的频率之比为1:2:3,已知报考“体育特长生”的学生人数是48,则体重在[50,55)组的频数为( )| A. | 36 | B. | 18 | C. | 12 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos(2x-1) | B. | -2cos(2x-1) | C. | 2cos(2x-1) | D. | -cos(2x-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${(\frac{1}{4})^2}×(\frac{3}{4})$ | B. | ${(\frac{3}{4})^2}×(\frac{1}{4})$ | C. | $C_3^2{(\frac{1}{4})^2}×(\frac{3}{4})$ | D. | $C_3^2{(\frac{3}{4})^2}×(\frac{1}{4})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com