
���� ��1����������4�ֽ��������ұȼ��2�֣���ͷ������ʤһ�֣�3��4����ʤ������������Ը��ʹ�ʽ���ɵý��ۣ�
��2����������ο��ܵ�ȡֵΪ2��4��6�������Ӧ�ĸ��ʣ��ɵæεķֲ��к���ѧ������
��� �⣺��1����������4�ֽ������Ҽױ��Ҷ��2�֣���ͷ���ּ�ʤһ�֣�3��4����ʤ��
���������ΪP=${C}_{2}^{1}��\frac{3}{4}����\frac{1}{4}����\frac{3}{4}����\frac{3}{4}��$=��
��2�������⣬�ε�ȡֵΪ2��4��6����
P����=2��=��$\frac{3}{4}$��2+��$\frac{1}{4}$��2=$\frac{5}{8}$��
P����=4��=${C}_{2}^{1}$��$\frac{1}{4}$����$\frac{3}{4}$����$\frac{3}{4}$��2+${C}_{2}^{1}$��$\frac{1}{4}$����$\frac{3}{4}$����$\frac{1}{4}$��2=$\frac{15}{64}$��
P����=6��=${C}_{2}^{1}��\frac{1}{4}����\frac{3}{4}��$•${C}_{2}^{1}��\frac{1}{4}����\frac{3}{4}��$=$\frac{9}{64}$��
��εķֲ���
| �� | 2 | 4 | 6 |
| P | $\frac{5}{8}$ | $\frac{15}{64}$ | $\frac{9}{64}$ |
���� ���⿼�����֪ʶ��������ɢ����������ķֲ�������ѧ������ȷ��������ȡֵ����ȷ������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
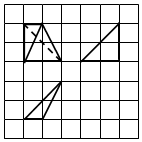 ��ͼ�������С�����εı߳���1���������ô�ʵ�ߺʹ���������ij�����������ͼ������������������ǣ�������
��ͼ�������С�����εı߳���1���������ô�ʵ�ߺʹ���������ij�����������ͼ������������������ǣ�������| A�� | 1 | B�� | $\frac{2}{3}$ | C�� | $\frac{4}{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��2�� | B�� | ��-1��2�� | C�� | ��-1��-2�� | D�� | ��1��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{10}{9}$ | B�� | 4 | C�� | $\frac{40}{9}$ | D�� | $\frac{56}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��l������y=f��x����x=4�������ߣ���f��4��+f�䣨4����ֵΪ5.5��
��ͼ��ֱ��l������y=f��x����x=4�������ߣ���f��4��+f�䣨4����ֵΪ5.5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{1}{2}$ | C�� | 3 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com