
【题目】已知斜三棱柱![]() 的侧面
的侧面![]() 与底
与底![]() 垂直,侧棱与底面所成的角为
垂直,侧棱与底面所成的角为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
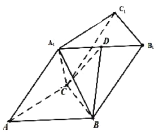
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为棱
为棱![]() 上的点,且三棱锥
上的点,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由面面垂直的性质定理得![]() 与平面
与平面![]() 垂直,从而有
垂直,从而有![]() ,因此可证明
,因此可证明![]() 与平面
与平面![]() 垂直,于是得证面面垂直;
垂直,于是得证面面垂直;
(2)由(1)中垂直关系得![]() 和
和![]() 都是直角三角形,找到
都是直角三角形,找到![]() 与底面所成的角后可计算出图中线段长,从而求得
与底面所成的角后可计算出图中线段长,从而求得![]() 面积,由
面积,由![]() 的体积计算出
的体积计算出![]() 到平面
到平面![]() 的距离
的距离![]() ,注意(1)中线面垂直,由
,注意(1)中线面垂直,由![]() 得
得![]() 是
是![]() 中点.从而得比值.
中点.从而得比值.
(1)证明:∵面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,![]()
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
(2)由(1)可知,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,![]()
又∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 在底面
在底面![]() 上的射影落在
上的射影落在![]() 上,
上,
所以![]() 就是侧棱
就是侧棱![]() 与底面
与底面![]() 所成的角,且
所成的角,且![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
设点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() ,
,
则![]() ,∴
,∴![]() ,
,
所以![]() ,所以点
,所以点![]() 是棱
是棱![]() 的中点,从而
的中点,从而![]() 为所求..
为所求..


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】如城某观光区的平面示意图如图所示,其中矩形![]() 的长
的长![]() 千米,宽
千米,宽![]() 千米,半圆的圆心
千米,半圆的圆心![]() 为
为![]() 中点.为了便于游客观光休闲,在观光区铺设一条由圆弧
中点.为了便于游客观光休闲,在观光区铺设一条由圆弧![]() 、线段
、线段![]() 、
、![]() 组成的观光道路.其中线段
组成的观光道路.其中线段![]() 经过圆心
经过圆心![]() ,且点
,且点![]() 在线段
在线段![]() 上(不含线段端点
上(不含线段端点![]() 、
、![]() ).已知道路
).已知道路![]() 、
、![]() 的造价为
的造价为![]() 元每千米,道路
元每千米,道路![]() 造价为
造价为![]() 元每千米,设
元每千米,设![]() ,观光道路的总造价为
,观光道路的总造价为![]() .
.
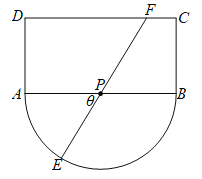
(1)试求![]() 与
与![]() 的函数关系式:
的函数关系式:![]() ;
;
(2)当![]() 为何值时,观光道路的总造价
为何值时,观光道路的总造价![]() 最小.
最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润增长 | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
(1)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程(结果保留两位小数);
的回归直线方程(结果保留两位小数);
(2)现从2012—2018年这7年中抽出三年进行调查,记![]() 年利润增长-投资金额,设这三年中
年利润增长-投资金额,设这三年中![]() (万元)的年份数为
(万元)的年份数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考公式: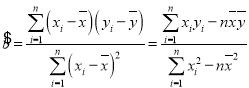 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长途车站P与地铁站O的距离为![]() 千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角
千米,从地铁站O出发有两条道路l1,l2,经测量,l1,l2的夹角为45°,OP与l1的夹角![]() 满足tan
满足tan![]() =
=![]() (其中0<θ<
(其中0<θ<![]() ),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.
),现要经过P修条直路分别与道路l1,l2交汇于A,B两点,并在A,B处设立公共自行车停放点.

(1)已知修建道路PA,PB的单位造价分别为2m元/千米和m元/千米,若两段道路的总造价相等,求此时点A,B之间的距离;
(2)考虑环境因素,需要对OA,OB段道路进行翻修,OA,OB段的翻修单价分别为n元/千米和![]() n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
n元/千米,要使两段道路的翻修总价最少,试确定A,B点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py经过点(2,1).
(Ⅰ)求抛物线C的方程及其准线方程;
(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N,直线y=1分别交直线OM,ON于点A和点B.求证:以AB为直径的圆经过y轴上的两个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为:(x-3)2+(y-2)2=r2(r>0),若直线3x+y=3上存在一点P,在圆C上总存在不同的两点M,N,使得点M是线段PN的中点,则圆C的半径r的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为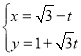 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康。经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加。为了更好的制定2019年关于加快提升农民年收人力争早日脱贫的工作计划,该地扶贫办统计了2018年![]() 位农民的年收人并制成如下频率分布直方图:
位农民的年收人并制成如下频率分布直方图:
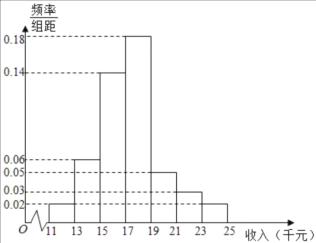
(1)根据频率分布直方图,估计![]() 位农民的年平均收入
位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求:
.利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的![]() 的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了![]() 位农民。若每个农民的年收人相互独立,问:这
位农民。若每个农民的年收人相互独立,问:这![]() 位农民中的年收入不少于
位农民中的年收入不少于![]() 千元的人数最有可能是多少?
千元的人数最有可能是多少?
附:参考数据与公式![]()
则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com