
| 届次 | 第26届(亚特兰大) | 第27届(悉尼) | 第28届(雅典) | 第29届(北京) | 第30届(伦敦) |
| 序号x | 1 | 2 | 3 | 4 | 5 |
| 金牌数y | 16 | 28 | 32 | 51 | 38 |
| 届次 | 第26届(亚特兰大) | 第27届(悉尼) | 第28届(雅典) | 第29届(北京) | 第30届(伦敦) |
| 序号x | 1 | 2 | 3 | 4 | 5 |
| 金牌数y | 16 | 28 | 32 | 51 | 38 |
| 预测值$\stackrel{∧}{y}$ | |||||
| y-$\stackrel{∧}{y}$ |
分析 (1)根据回归方程$\stackrel{∧}{y}$=5.0857x+14.514,计算x=6时$\stackrel{∧}{y}$的值;
(2)根据题中数据,计算$\overline{x}$、$\overline{y}$与$\stackrel{∧}{b}$、$\stackrel{∧}{a}$的值,得出回归方程$\stackrel{∧}{y}$=6.7x+12.9,并计算x=6时$\stackrel{∧}{y}$的值;
(3)利用(2)的结论填表,得出|y-$\stackrel{∧}{y}$|≤4的数据,求X的分布列与数学期望值.
解答 解:(1)根据金牌数$\stackrel{∧}{y}$关于序号x的回归方程为$\stackrel{∧}{y}$=5.0857x+14.514,
所以x=6时,$\stackrel{∧}{y}$=5.0857×6+14.514≈45,
据此回归方程预测第31届夏季奥运会中国队获得的金牌数45;
(2)根据上述五组数据,计算$\overline{x}$=$\frac{1}{5}$×(1+2+3+4+5)=3,
$\overline{y}$=$\frac{1}{5}$×(16+28+32+51+38)=33;
$\stackrel{∧}{b}$=$\frac{(1-3)(16-33)+(2-3)(28-33)+(3-3)(32-33)+(4-3)(51-33)+(5-3)(38-33)}{{(1-3)}^{2}{+(2-3)}^{2}{+(3-3)}^{2}{+(4-3)}^{2}{+(5-3)}^{2}}$=6.7,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=33-6.7×3=12.9.
金牌数$\stackrel{∧}{y}$关于序号x的回归方程$\stackrel{∧}{y}$=6.7x+12.9,
x=6,$\stackrel{∧}{y}$=6.7×6+12.9≈53,
预测第31届夏季奥林匹克运动会中国队获得的金牌数53;
(3)利用(2)的结论填写下表(结算结果四舍五入,保留整数):
| 届次 | 第26届(亚特兰大) | 第27届(悉尼) | 第28届(雅典) | 第29届(北京) | 第30届(伦敦) |
| 序号x | 1 | 2 | 3 | 4 | 5 |
| 金牌数y | 16 | 28 | 32 | 51 | 38 |
| 预测值$\stackrel{∧}{y}$ | 19 | 26 | 33 | 40 | 46 |
| y-$\stackrel{∧}{y}$ | -3 | 2 | -1 | 11 | -8 |
| X | 1 | 2 | 3 |
| P | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
点评 本题考查了古典概型的概率以及离散型随机变量的分布列与数学期望的计算问题,是综合性题目.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
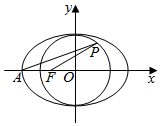 如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),⊙O:x2+y2=b2,点A、F分别是椭圆C的左顶点和左焦点,点P是⊙O上的动点,且$\frac{{|{PA}|}}{{|{PF}|}}$为定值,则椭圆C的离心率为( )
如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),⊙O:x2+y2=b2,点A、F分别是椭圆C的左顶点和左焦点,点P是⊙O上的动点,且$\frac{{|{PA}|}}{{|{PF}|}}$为定值,则椭圆C的离心率为( )| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6±2$\sqrt{35}$ | B. | 2±$\sqrt{35}$ | C. | 8±$\sqrt{35}$ | D. | 1±$\sqrt{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A(2,0)是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)长轴右端点,点B,C在椭圆C上,BC过椭圆O,$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,|$\overrightarrow{OC}$|=|$\overrightarrow{AC}$|,M,N为椭圆上异于A,B的不同两点,∠MCN的角平分线垂直于x轴.
如图,A(2,0)是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)长轴右端点,点B,C在椭圆C上,BC过椭圆O,$\overrightarrow{AC}$•$\overrightarrow{BC}$=0,|$\overrightarrow{OC}$|=|$\overrightarrow{AC}$|,M,N为椭圆上异于A,B的不同两点,∠MCN的角平分线垂直于x轴.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
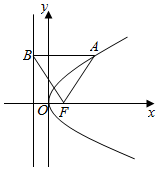 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若△ABF为等边三角形,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若△ABF为等边三角形,则抛物线的标准方程是( )| A. | y2=$\frac{1}{2}$x | B. | y2=x | C. | y2=2x | D. | y2=4x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某次数学小测验中(满分100分),某班50名学生得分如下面的频率分布直方图所示:
某次数学小测验中(满分100分),某班50名学生得分如下面的频率分布直方图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com