
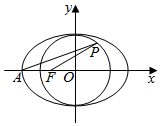
 如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),⊙O:x2+y2=b2,点A、F分别是椭圆C的左顶点和左焦点,点P是⊙O上的动点,且$\frac{{|{PA}|}}{{|{PF}|}}$为定值,则椭圆C的离心率为( )
如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),⊙O:x2+y2=b2,点A、F分别是椭圆C的左顶点和左焦点,点P是⊙O上的动点,且$\frac{{|{PA}|}}{{|{PF}|}}$为定值,则椭圆C的离心率为( )| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
分析 设P(x1,y1),由$\frac{{|{PA}|}}{{|{PF}|}}$是常数,得$({x}_{1}+a)^{2}+{{y}_{1}}^{2}=λ[({x}_{1}+c)^{2}+{{y}_{1}}^{2}]$,然后利用$x_1^2+y_1^2={b^2}$,转化为关于x1 的方程,由系数相等可得a,c的关系式,从而求得椭圆C的离心率.
解答 解:设F(-c,0),c2=a2-b2,
设P(x1,y1),要使得$\frac{{|{PA}|}}{{|{PF}|}}$是常数,则有$({x}_{1}+a)^{2}+{{y}_{1}}^{2}=λ[({x}_{1}+c)^{2}+{{y}_{1}}^{2}]$,λ是常数,
∵$x_1^2+y_1^2={b^2}$,
∴${b^2}+2a{x_1}+{a^2}=λ({b^2}+2c{x_1}+{c^2})$,
比较两边系数得b2+a2=λ(b2+c2),a=λc,
故c(b2+a2)=a(b2+c2),即2ca2-c3=a3,
即e3-2e+1=0,即(e-1)(e2+e-1)=0,
又0<e<1,
∴$e=\frac{{\sqrt{5}-1}}{2}$.
故选:D.
点评 本题考查椭圆的简单性质,考查数学转化思想方法,利用$\frac{{|{PA}|}}{{|{PF}|}}$为定值得到a,c的关系是解答该题的关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{3}$,1] | B. | [1,9] | C. | [$\frac{2}{3}$,9] | D. | [$\frac{\sqrt{6}}{3}$,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≥1 | B. | k>1 | C. | k≥2 | D. | k>2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲校 | 乙校 | 丙校 | |
| 男生 | 97 | 90 | x |
| 女生 | 153 | y | z |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 届次 | 第26届(亚特兰大) | 第27届(悉尼) | 第28届(雅典) | 第29届(北京) | 第30届(伦敦) |
| 序号x | 1 | 2 | 3 | 4 | 5 |
| 金牌数y | 16 | 28 | 32 | 51 | 38 |
| 届次 | 第26届(亚特兰大) | 第27届(悉尼) | 第28届(雅典) | 第29届(北京) | 第30届(伦敦) |
| 序号x | 1 | 2 | 3 | 4 | 5 |
| 金牌数y | 16 | 28 | 32 | 51 | 38 |
| 预测值$\stackrel{∧}{y}$ | |||||
| y-$\stackrel{∧}{y}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com