
分析 (1)利用绝对值三角不等式求出f(x)的最小值,即可求t的取值范围;
(2)求出t的最大值为T,化简a2+b2=T,利用基本不等式证明:$\frac{2}{{\frac{1}{a}+\frac{1}{b}}}$≤$\frac{{\sqrt{6}}}{2}$.
解答 解:(1)f(x)=|x+1|+|2-x|≥|x+1+2-x|=3,所以t≤3.(5分)
(2)证明:由(1)知T=3,所以a2+b2=3(a>0,b>0)
因为a2+b2≥2ab,所以$ab≤\frac{3}{2}$,又因为$\frac{1}{a}+\frac{1}{b}≥\frac{2}{{\sqrt{ab}}}$,
所以$\frac{2}{{\frac{1}{a}+\frac{1}{b}}}≤\sqrt{ab}≤\frac{{\sqrt{6}}}{2}$(当且仅当a=b时取“=”).(10分)
点评 本题考查绝对值不等式的值应用,基本不等式的应用,考查逻辑推理能力以及计算能力,转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{8}{15}$ | C. | $\frac{16}{15}$ | D. | $\frac{8}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}$+y2=1 | B. | $\frac{x^2}{3}$+y2=1 | C. | $\frac{x^2}{2}$+y2=1 | D. | $\frac{x^2}{4}$+$\frac{y^2}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
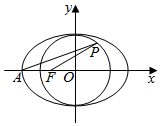 如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),⊙O:x2+y2=b2,点A、F分别是椭圆C的左顶点和左焦点,点P是⊙O上的动点,且$\frac{{|{PA}|}}{{|{PF}|}}$为定值,则椭圆C的离心率为( )
如图所示,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),⊙O:x2+y2=b2,点A、F分别是椭圆C的左顶点和左焦点,点P是⊙O上的动点,且$\frac{{|{PA}|}}{{|{PF}|}}$为定值,则椭圆C的离心率为( )| A. | $\frac{{\sqrt{2}-1}}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com