
分析 (Ⅰ)运用椭圆的定义可得a=2,由离心率公式可得c,再由a,b,c的关系可得b,进而得到椭圆方程;
(Ⅱ)由题意可得k=m,设点P(x1,y1),Q(x2,y2),联立直线方程和椭圆方程,消去y,可得x的方程,运用韦达定理和等比数列的中项的性质,化简整理可得k的值,进而得到所求直线的方程.
解答 解:(Ⅰ)由椭圆的定义可得|PF1|+|PF2|=2a=4,可得a=2,
由e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,可得c=$\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
则椭圆方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)由直线y=kx+m经过点(-1,0),可知,k=m,
设点P(x1,y1),Q(x2,y2),
由$\left\{\begin{array}{l}y=kx+k\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$,消y,得(4k2+1)x2+8k2x+4k2-4=0,
由直线与椭圆交于不同的两点,可得△=64k4-16(k2-1)(4k2+1)>0,解得k∈R,
由韦达定理得,${x_1}+{x_2}=-\frac{{8{k^2}}}{{4{k^2}+1}}$,${x_1}{x_2}=\frac{{4{k^2}-4}}{{4{k^2}+1}}$,
由题意知,k2=kOP•kOQ,
即${k^2}=\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=\frac{{{k^2}{x_1}{x_2}+{k^2}({x_1}+{x_2})+{k^2}}}{{{x_1}{x_2}}}={k^2}+\frac{{{k^2}({x_1}+{x_2})}}{{{x_1}{x_2}}}+\frac{k^2}{{{x_1}{x_2}}}$,
所以$\frac{{{k^2}({x_1}+{x_2})}}{{{x_1}{x_2}}}+\frac{k^2}{{{x_1}{x_2}}}=0$,即-$\frac{8{k}^{2}}{1+4{k}^{2}}$+1=0,
即${k^2}=\frac{1}{4}$,即为k=±$\frac{1}{2}$,
所以直线l的方程为x-2y+1=0或x+2y+1=0.
点评 本题考查椭圆的方程的求法,注意运用椭圆的定义和离心率公式,考查直线方程和椭圆方程联立,运用韦达定理,以及等比数列的中项的性质和直线的斜率公式,考查化简整理的运算能力,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
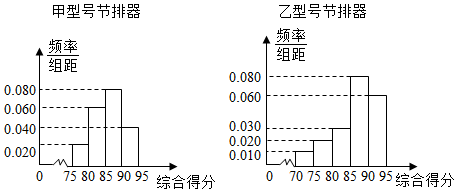
| 综合得分k的取值范围 | 节排器等级 | 节排器利润率 |
| k≥85 | 一级品 | a |
| 75≤k<85 | 二级品 | 5a2 |
| 70≤k<75 | 三级品 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [10,25) | [25,40) | [40,55] |
| 成绩优秀 | 670 | a | b |
| 成绩一般 | 80 | 60 | c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 产品编号 | ① | ② | ③ | ④ | ⑤ |
| 电压(x) | 10 | 15 | 20 | 25 | 30 |
| 电流(y) | 0.6 | 0.8 | 1.4 | 1.2 | 1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com