
【题目】设函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)求函数![]() 的单调递增区间及对称中心;
的单调递增区间及对称中心;
(3)函数![]() 可以由
可以由![]() 经过怎样的变换得到.
经过怎样的变换得到.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)见解析.
;(3)见解析.
【解析】
分析:根据正弦的两角和公式与辅助角公式将![]() 化简为
化简为![]() 或
或![]() .
.
. (1)结合最小正周期计算公式![]() ,得最小正周期;
,得最小正周期;
(2)解法一:利用余弦函数单调性解不等式,可得函数![]() 的递增区间;再由余弦函数的对称中心解方程,可得函数
的递增区间;再由余弦函数的对称中心解方程,可得函数![]() 的对称中心;
的对称中心;
解法二:利用正弦函数单调性解不等式,可得函数![]() 的递增区间;再由正弦函数的对称中心解方程,可得函数
的递增区间;再由正弦函数的对称中心解方程,可得函数![]() 的对称中心;
的对称中心;
(3)解法一:将函数![]() 的图象向右平移
的图象向右平移![]() ,横坐标压缩到原来的
,横坐标压缩到原来的![]() ,纵坐标拉伸到原来的2倍,即可得到函数
,纵坐标拉伸到原来的2倍,即可得到函数![]() 的图象.
的图象.
解法二:将函数![]() 的图象向右平移
的图象向右平移![]() ,横坐标压缩到原来的
,横坐标压缩到原来的![]() ,纵坐标拉伸到原来的2倍,即可得到函数
,纵坐标拉伸到原来的2倍,即可得到函数![]() 的图象.
的图象.
详解:解:解法一
因为![]() ,
,
所以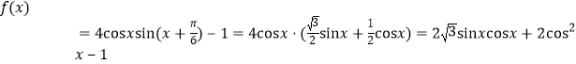
![]() .
.
(1)因为![]() , 所以
, 所以![]() .
.
(2)由![]() ,
,
所以函数的单调递增区间为:![]() ,
,
由![]() ,
,
所以对称中心为:![]() .
.
(3)函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象
的图象
函数![]() 的图象上的每一点的纵坐标不变,横坐标变为原来的
的图象上的每一点的纵坐标不变,横坐标变为原来的![]() ,得到函数
,得到函数![]()
函数![]() 的图象上的每一点的横坐标不变,纵坐标变为原来的倍2
的图象上的每一点的横坐标不变,纵坐标变为原来的倍2
得到函数![]() 的图象.
的图象.
解法二
因为![]() ,
,
所以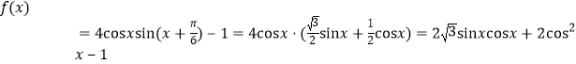 ,
,
![]()
(1)因为![]() , 所以
, 所以![]()
(2)由![]()
所以函数的单调递增区间为:![]()
由![]() ,
,
所以对称中心为:![]() .
.
(3)函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象
的图象
函数![]() 的图象上的每一点的纵坐标不变,横坐标变为原来的
的图象上的每一点的纵坐标不变,横坐标变为原来的![]() ,
,
得到函数![]() 。
。
函数![]() 的图象上的每一点的横坐标不变,纵坐标变为原来的倍2,
的图象上的每一点的横坐标不变,纵坐标变为原来的倍2,
得到函数![]() 的图象.
的图象.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.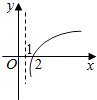
B.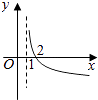
C.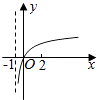
D.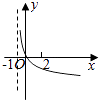
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】奥地利遗传学家孟德尔1856年用豌豆作实验时,他选择了两种性状不同的豌豆,一种是子叶颜色为黄色,种子性状为圆形,茎的高度为长茎,另一种是子叶颜色为绿色,种子性状为皱皮,茎的高度为短茎。我们把纯黄色的豌豆种子的两个特征记作![]() ,把纯绿色的豌豆的种子的两个特征记作
,把纯绿色的豌豆的种子的两个特征记作![]() ,实验杂交第一代收获的豌豆记作
,实验杂交第一代收获的豌豆记作![]() ,第二代收获的豌豆出现了三种特征分别为
,第二代收获的豌豆出现了三种特征分别为![]() ,
,![]() ,
,![]() ,请问,孟德尔豌豆实验第二代收获的有特征
,请问,孟德尔豌豆实验第二代收获的有特征![]() 的豌豆数量占总收成的( )
的豌豆数量占总收成的( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在框图中,设x=2,并在输入框中输入n=4;ai=i(i=0,1,2,3,4).则此程序执行后输出的S值为( )

A. 26 B. 49 C. 52 D. 98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)的影响,对近六年的年宣传费
(单位:吨)的影响,对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年宣传费 | 23 | 25 | 27 | 29 | 32 | 35 |
年销售量 | 11 | 21 | 24 | 66 | 115 | 325 |
(1)根据散点图判断![]() 与
与![]() ,哪一个更适合作为年销售量
,哪一个更适合作为年销售量![]() (吨)与关于宣传费
(吨)与关于宣传费![]() (万元)的回归方程类型;
(万元)的回归方程类型;
(2)规定当产品的年销售量![]() (吨)与年宣传费
(吨)与年宣传费![]() (万元)的比值大于1时,认为该年效益良好,现从这6年中任选3年,记其中选到效益良好的数量为
(万元)的比值大于1时,认为该年效益良好,现从这6年中任选3年,记其中选到效益良好的数量为![]() ,试求
,试求![]() 的所有取值情况及对应的概率;
的所有取值情况及对应的概率;
(3)根据频率分布直方图中求出样本数据平均数的思想方法,求![]() 的平均数.
的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC所在的平面内,点P0、P满足 ![]() =
= ![]()
![]() ,
, ![]() ,且对于任意实数λ,恒有
,且对于任意实数λ,恒有 ![]()
![]() ,则( )
,则( )
A.∠ABC=90°
B.∠BAC=90°
C.AC=BC
D.AB=AC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 过圆上任意一点
过圆上任意一点![]() 向
向![]() 轴引垂线垂足为
轴引垂线垂足为![]() (点
(点![]() 、
、![]() 可重合),点
可重合),点![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 的轨迹方程为曲线
的轨迹方程为曲线![]() ,不过原点
,不过原点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,满足直线
两点,满足直线![]() ,
, ![]() ,
, ![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在坐标原点,焦点在坐标轴上,且经过
中心在坐标原点,焦点在坐标轴上,且经过![]() 三点.
三点.
(1)求椭圆![]() 的方程;
的方程;
(2)在直线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,分别与椭圆
,分别与椭圆![]() 交于
交于![]() 两点,判断直线
两点,判断直线![]() 是否过定点?若是,求出该定点.若不是,请说明理由.
是否过定点?若是,求出该定点.若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cosθ,直线l的参数方程为  (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程及直线l的普通方程;
(2)若曲线C2的参数方程为 ![]() (α为参数),曲线C1上点P的极角为
(α为参数),曲线C1上点P的极角为 ![]() ,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
,Q为曲线C2上的动点,求PQ的中点M到直线l距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com