Question

18．如图，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F₁、F₂，离心率e=$\frac{1}{2}$．过F₂的直线交椭圆C于A、B两点，且△ABF₁的周长为8．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l：y=kx+m与椭圆C相切于P点，且与直线x=-4相交于Q点，求证：直线PF₁垂直于直线QF₁．

Answer 1

分析 （Ⅰ）运用椭圆的定义，可得a=2，再由离心率公式，可得c，由a，b，c的关系，可得b，进而得到椭圆方程；
（Ⅱ）直线l：y=kx+m代入椭圆方程，运用直线和椭圆相切的条件：判别式为0，可得切点P的坐标，再令x=-4，可得Q的坐标，运用两直线垂直的条件：斜率之积为-1，即可得证．

解答 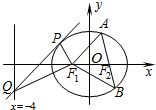（Ⅰ）解：∵|AB|+|AF₁|+|BF₁|=8，
即|AF₁|+|AF₂|+|BF₁|+|BF₂|=8，
而|AF₁|+|AF₂|=|BF₁|+|BF₂|=2a，
∴4a=8，即a=2．
∵$e=\frac{c}{a}=\frac{1}{2}$，
∴c=1，则$b=\sqrt{{a^2}-{c^2}}=\sqrt{3}$．
∴椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$．
（Ⅱ）证明：由$\left\{{\begin{array}{l}{y=kx+m{，_{\;}}}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$得（4k²+3）x²+8kmx+4m²-12=0．
如图，设P点的坐标为（x₀，y₀），依题意m≠0且△=0，
即△=64k²m²-4（4k²+3）（4m²-12）=0，
整理得4k²+3=m²．
此时${x_0}=-\frac{4km}{{4{k^2}+3}}=-\frac{4k}{m}$，${y_0}=k{x_0}+m=-\frac{{4{k^2}}}{m}+m=\frac{3}{m}$，
∴P点的坐标为$（-\frac{4k}{m}{，_{\;}}\frac{3}{m}）$． 
由$\left\{{\begin{array}{l}{y=kx+m{，_{\;}}}\\{x=-4}\end{array}}\right.$解得y=-4k+m．
∴Q点的坐标为（-4，-4k+m）．
由F₁（-1，0），求得${k_{P{F_1}}}=\frac{{\frac{3}{m}-0}}{{-\frac{4k}{m}+1}}=\frac{3}{m-4k}$，
${k_{Q{F_1}}}=\frac{-4k+m-0}{-4+1}=-\frac{m-4k}{3}$，
∴${k_{P{F_1}}}•{k_{Q{F_1}}}=-1$．
∴直线PF₁垂直于直线QF₁．

点评 本题考查椭圆的定义和方程，性质，主要考查定义和离心率公式及方程的运用，注意联立直线方程，运用直线和椭圆相切的条件：判别式为0，同时考查两直线垂直的条件，属于中档题．