
����Ŀ��ij��Ϊ���ռ�����֪ʶ����ǿ����ķ��ƹ����Ա����ض���Ⱥ�ٰ�����ѧ���շ�����.Ϊ�˽�ο���Ⱥ�ķ���֪ʶˮƽ����һ���շ������������ȡ��50�ݴ�����з������õ���50�ݴ���ɼ���ͳ����������:
�ɼ����� |
|
|
|
|
|
|
Ƶ�� | 2 | 5 | 12 | 16 | 10 | 5 |
(1)�ڴ����ͼ�������������ݵ�Ƶ�ʷֲ�ֱ��ͼ��
(2)�Ը���ͳ�����ݣ����Ʊ����շ����Ե�ƽ���ɼ�![]() ����λ��( ͬһ���е������ø���������е�ֵ������)��
����λ��( ͬһ���е������ø���������е�ֵ������)��
(3)��֪������100 ���˲μӿ��ԣ��÷ֵ���60 �ֵ���Ҫ�ؿ�(������60 ��Ϊ�ϸ����ؿ�)����ÿ���ؿ��ĺϸ��ʶ�����һ�ο��Ե�6 ���ٷֵ㣬�Թ��Ƶ�3 ���ؿ�������.
���𰸡���1������������2��73.75����3��0.728
�������������������1���ȼ����ÿһ���Ƶ�ʣ��ټ����![]() ����ͼ���������ɣ���2��������е�ֵ����ӦƵ�ʣ�����ƽ������ʽ��������ɣ���λ����Ϊ
����ͼ���������ɣ���2��������е�ֵ����ӦƵ�ʣ�����ƽ������ʽ��������ɣ���λ����Ϊ![]() �Ľ⣻��3�������ڳ��ο��Ժ���Ҫ�ؿ��ĸ���
�Ľ⣻��3�������ڳ��ο��Ժ���Ҫ�ؿ��ĸ���![]() ����2���ؿ�����Ҫ�ؿ��ĸ���
����2���ؿ�����Ҫ�ؿ��ĸ���![]() ���ʶ��ɼ�������.
���ʶ��ɼ�������.
�����������1��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ
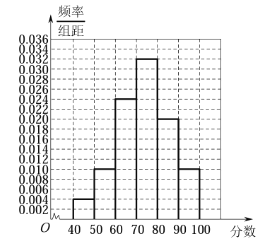
��2���������ݸ����е�ֵ����Ӧ��Ƶ�����£�
������ֵ | 45 | 55 | 65 | 75 | 85 | 95 |
Ƶ�� | 0.04 | 0.1 | 0.24 | 0.32 | 0.2 | 0.1 |
�շ����Ե�ƽ���ɼ�![]() ���������ɼ�����λ��Ϊ
���������ɼ�����λ��Ϊ![]() ������֪
������֪![]() ����
����![]() ����
����![]() ���ɴ˹��ƣ������շ����Գɼ�����λ��Ϊ73.75.
���ɴ˹��ƣ������շ����Գɼ�����λ��Ϊ73.75.
��3���ڳ��ο��Ժ÷ֵ���60�ֵ�Ƶ��Ϊ![]() ���ɴ˹����ڳ��ο��Ժ���Ҫ�ؿ��ĸ���
���ɴ˹����ڳ��ο��Ժ���Ҫ�ؿ��ĸ���![]() ��������֪����1���ؿ�����Ҫ�ؿ��ĸ���
��������֪����1���ؿ�����Ҫ�ؿ��ĸ���![]() ����2���ؿ�����Ҫ�ؿ��ĸ���
����2���ؿ�����Ҫ�ؿ��ĸ���![]() �����ԣ���3���ؿ�����������Ϊ
�����ԣ���3���ؿ�����������Ϊ![]() �����ˣ�
�����ˣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����רҵ400��ѧ���μ�ij�β�����������Ůѧ������������ʹ�÷ֲ�����ķ������������ȡ��100��ѧ������¼���ǵķ����������ݷֳ�7�飺[20,30����[30,40��������[80,90]���������õ�����Ƶ�ʷֲ�ֱ��ͼ��
���������400��ѧ���������ȡһ�ˣ����������С��70�ĸ��ʣ�
������֪�����з���С��40��ѧ����5�ˣ��Թ��������з���������[40,50���ڵ�������
��������֪��������һ�������ķ�����С��70���������з�����С��70����Ů��������ȣ��Թ���������������Ů�������ı�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ABC��A1B1C1�У���ACB=90�㣬2AC=AA1=BC=2���������B1��DC��C1�Ĵ�СΪ60�㣬��AD�ij�Ϊ�� �� 
A.![]()
B.![]()
C.2
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����C1�� ![]() =1����a��0��b��0���Ľ�����ʵ�᳤��2������������C2��x2=2py����p��0���Ľ��㵽˫����C1�Ľ����ߵľ���Ϊ2����������C2�ı����̣�
=1����a��0��b��0���Ľ�����ʵ�᳤��2������������C2��x2=2py����p��0���Ľ��㵽˫����C1�Ľ����ߵľ���Ϊ2����������C2�ı����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯�� A={x|2��x��4}��B={a��x��3a}��
��1����A��B������ʵ��a�ķ�Χ��
��2����A��B={x|2��x��6}����ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ2��������ABCD�У���E��AB���е㣬��F��BC���е㣬����AED����DCF�ֱ���DE��DF����ʹA��C�����غ��ڵ�A�䣬����EF��A��B�� 
��1����֤��A��D��EF��
��2��������A�䩁EF��D������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��= ![]() ��������x�ķ���f2��x��+bf��x��+c=0ǡ��5����ͬ��ʵ����x1 �� x2 �� x3 �� x4 �� x5 �� h��x��=lg|x��4|����h��x1+x2+x3+x4+x5�����ڣ� ��
��������x�ķ���f2��x��+bf��x��+c=0ǡ��5����ͬ��ʵ����x1 �� x2 �� x3 �� x4 �� x5 �� h��x��=lg|x��4|����h��x1+x2+x3+x4+x5�����ڣ� ��
A.3
B.lg12
C.lg20
D.4lg2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() .
.
��1����![]() ����
����![]() �ĵ������䣻
�ĵ������䣻
��2����֪![]() ��
��![]() ��ȡ�ü���ֵ.��ʵ��
��ȡ�ü���ֵ.��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ������
������![]()
![]()
��1����![]() ʱ�������
ʱ�������![]() �IJ���ʽ��
�IJ���ʽ�� ![]() ��
��
��2����![]() ��
��![]() ����֪����
����֪����![]() ���������
���������![]() ��
��![]() ������
������![]() ��
�� ![]() ������
������![]() ������ԭ�㣬֤����
������ԭ�㣬֤���� ![]() ��
��![]() �����ܴ�ֱ.
�����ܴ�ֱ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com