
| 2x2-bx+1 |
| x |
| 1 |
| x |
| 1 |
| x |
| f(x2)-f(x1) |
| x2-x1 |
cln
| ||
| x2-x1 |
ln
| ||
| x2-x1 |
| 2 |
| x2+x1 |
| x2 |
| x1 |
| lnt |
| t-1 |
| 2 |
| t+1 |
| 2t-2 |
| t+1 |
| 2x2-bx+1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| f(x2)-f(x1) |
| x2-x1 |
| a( x22-x12)+b(x2-x1) |
| x2-x1 |
| g(x2)-g(x1) |
| x2-x1 |
a( x22-x12)+b(x2-x1)+c•ln
| ||
| x2-x1 |
cln
| ||
| x2-x1 |
| c |
| x0 |
cln
| ||
| x2-x1 |
| c |
| x0 |
ln
| ||
| x2-x1 |
| 2 |
| x2+x1 |
| x2 |
| x1 |
| lnt |
| t-1 |
| 2 |
| t+1 |
| 2t-2 |
| t+1 |
| 1 |
| t |
| 2(t+1)-2(t-1) |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
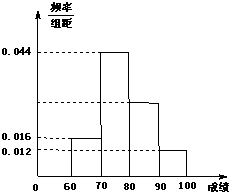 某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.
某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
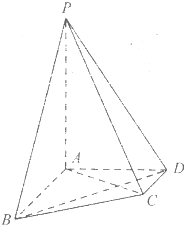 在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2
在四棱锥p-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2| 2 |
| ||
| 3 |
| PQ |
| PB |
查看答案和解析>>
科目:高中数学 来源: 题型:
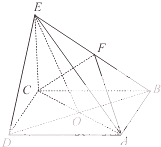 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.| 2 |
| EG |
| EO |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com