
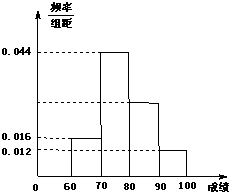
 某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.
某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.| C | 1 3 |
| C | 1 2 |
| C | 1 3 |
| X | 2 | 3 | 4 |
| P | 0.16 | 0.192 | 0.648 |


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
| 5 |
| 2 |
| 5an-8 |
| 2an-3 |
| 1 |
| an-2 |
| 9 |
| 10 |
| Sn |
| n+4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
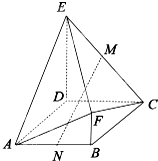 多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=
多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=查看答案和解析>>
科目:高中数学 来源: 题型:
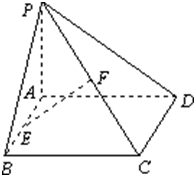 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
| RP |
| RQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com