
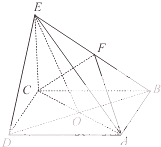
 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.| 2 |
| EG |
| EO |
| 2 |
 (1)证明:连接OF,由四边形ABCD是正方形可知,点O为BD的中点,
(1)证明:连接OF,由四边形ABCD是正方形可知,点O为BD的中点,| 2 |
| ||
| 2 |
| EG |
| EO |
| 1 |
| 2 |


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 6 |
| y2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
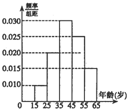 某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示:
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示:| 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 | |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | a | 0.9 |
| 第3组 | [35,45) | 27 | x |
| 第4组 | [45,55) | b | 0.36 |
| 第5组 | [55,65) | 3 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
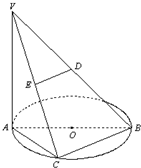 如图,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.
如图,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
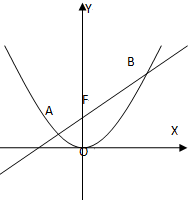 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com