练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    为了调查喜爱运动是否和性别有关，我们随机抽取了50名对象进行了问卷调查得到了如下的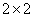列联表:

    若在全部50人中随机抽取2人,抽到喜爱运动和不喜爱运动的男性各一人的概率为.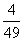

    (1)请将上面的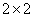列联表补充完整；

    (2)能否在犯错误的概率不超过0.001的前提下认为喜爱运动与性别有关?说明你的理由.

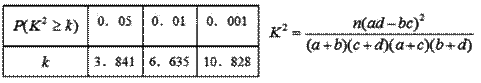    附:


    解:(1)设喜爱运动的男性有人，由题意可知

    ，解得，             

    所以填表如下

    喜爱运动

    不喜爱运动

    合 计

    男性

    20

    5

    25

    女性

    10

    15

    25

    合计

    30

    20

    50

    (2)

                                                                                   

    故不能在犯错误的概率不超过0.001的前提下认为推断喜爱运动与性别有关.                                           


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在平面直角坐标系中，定义d（P，Q）=|x1﹣x2|+|y1﹣y2|为两点P（x1，y1），Q（x2，y2）之间的“折线距离”，在这个定义下，给出下列命题：

    ①到原点的“折线距离”等于1的点的集合是一个圆；

    ②到原点的“折线距离”小于等于2的点构成的区域面积为8；

    ③到M（0，﹣2），N（0，2）两点的“折线距离”相等的点的轨迹方程是y=0；

    ④直线y=x+1上的点到N（0，2）的“折线距离”的最小值为1．

    其中真命题有（　　）

    　

    A．

    1个

    B．

    2个

    C．

    3个

    D．

    4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若实数成等比数列，非零实数分别为与，与的等差中项，则下列结论正确的是                                                          

    A．        B．      C．      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     某款手机的广告宣传费用x（单位万元）与利润y（单位万元）的统计数据如下表：

    广告宣传费用x

    6

    5

    7

    8

    利润y

    34

    26

    38

    42

    根据上表可得线性回归方程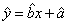中的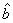为9.4，据此模型预报广告宣传费用为10万元时利润为                                                        

    A．65.0万元       B．67.9万元       C．68.1万元         D．68.9万元

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设随机变量服从正态分布,若,则   

    查看答案和解析>>

    科目：高中数学 来源： 题型：


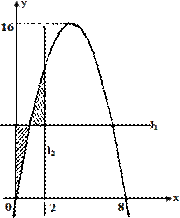      　　　  已知二次函数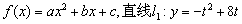(其中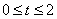,t为常数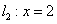）,的图象如图所示.

       （1）根据图象求a、b、c的值；

       （2）求阴影面积S关于t的函数S(t)的解析式；

       （3）若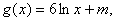问是否存在实数m， 使得

    的图象与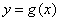的图象有且只有三个不同的

    交点？若存在，求出m的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在某个城市中，M，N两地之间有南北街道5条、东西街道4条，现要求沿图中的街道，以最短的路程从M走到N，则不同的走法共有　_________　种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知{an}是公比为q的等比数列，且a1，a3，a2成等差数列，则q＝      (    )

    A.1或－          B.1                 C.－              D.－2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在数列中，=1，，则的值为 （   ）

    A．99            B．49            C．102          D． 101

    查看答案和解析>>

    同步练习册答案