
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,下列四个命题中不正确的命题是( )
A.若![]() ,则△ABC一定是等边三角形
,则△ABC一定是等边三角形
B.若![]() ,则△ABC一定是锐角三角形
,则△ABC一定是锐角三角形
C.若![]() ,则△ABC一定是等腰三角形
,则△ABC一定是等腰三角形
D.若![]() ,则△ABC一定是等腰三角形或直角三角形
,则△ABC一定是等腰三角形或直角三角形
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.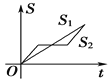 B.
B.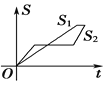 C.
C.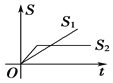 D.
D.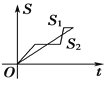
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 部分图象如图所示.
部分图象如图所示. 
(Ⅰ)求φ值及图中x0的值;
(Ⅱ)在△ABC中,A,B,C的对边分别为a,b,c,已知 ![]() ,f(C)=﹣2,sinB=2sinA,求a的值.
,f(C)=﹣2,sinB=2sinA,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有除颜色外完全相同的红、黄、白三种颜色的球各一个,从中每次任取1个.有放回地抽取3次,求:
(1)3个全是红球的概率. (2)3个颜色全相同的概率.
(3)3个颜色不全相同的概率. (4)3个颜色全不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C:x2=2py(p>0)的焦点为F,过F的直线l交C于A,B两点,交x轴于点D,B到x轴的距离比|BF|小1.
(Ⅰ)求C的方程;
(Ⅱ)若S△BOF=S△AOD , 求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出程序框图中①,②,③处应填充的式子.
(2)若输出的面积y值为6,则路程x的值为多少?


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(﹣1,0),B(1,0), ![]() =
= ![]() +
+ ![]() ,|
,| ![]() |+|
|+| ![]() |=4
|=4
(1)求P的轨迹E
(2)过轨迹E上任意一点P作圆O:x2+y2=3的切线l1 , l2 , 设直线OP,l1 , l2的斜率分别是k0 , k1 , k2 , 试问在三个斜率都存在且不为0的条件下, ![]() (
( ![]() +
+ ![]() )是否是定值,请说明理由,并加以证明.
)是否是定值,请说明理由,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com