
已知函数f(x)=ax-ln x,g(x)=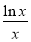 ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
(1)当a=1时,求函数f(x)的最小值;
(2)当a=1时,求证:f(m)>g(n)+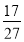 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立;
(3)是否存在实数a,使得f(x)的最小值是3?如果存在,求出a的值;如果不存在,说明理由.
(1)1 (2)见解析 (3)见解析
【解析】【解析】
(1)当a=1时,f(x)=x-ln x.
所以f′(x)=1-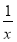 .
.
令f′(x)=0,得x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
x | (0,1) | 1 | (1,e] |
f′(x) | - | 0 | + |
f(x) | ? | 1 | ? |
所以当x=1时,f(x)min=1.
(2)证明:由(1)知,当m∈(0,e]时,
有f(m)≥1.
因为0<x≤e,所以g′(x)=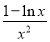 ≥0,
≥0,
即g(x)在区间(0,e]上为增函数,
所以g(x)≤g(e)=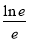 =
=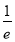 <
<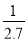 =
=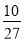 ,
,
所以g(x)+ <
<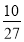 +
+ =1,
=1,
所以当m,n∈(0,e]时,
g(n)+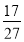 <1≤f(m).
<1≤f(m).
所以f(m)>g(n)+ 对一切m,n∈(0,e]恒成立.
对一切m,n∈(0,e]恒成立.
(3)假设存在实数a,使f(x)的最小值是3,则
f′(x)=a- =
=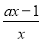 .
.
①当a≤ 时,因为0<x≤e,所以ax≤1,
时,因为0<x≤e,所以ax≤1,
所以f′(x)≤0,所以f(x)在(0,e]上为减函数.
所以当x=e时,fmin(x)=ae-1=3,
解得a= (舍去);
(舍去);
②当a>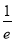 时,
时,
若0<x<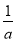 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在 上为减函数;
上为减函数;
若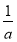 <x≤e时,f′(x)>0,f(x)在
<x≤e时,f′(x)>0,f(x)在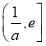 上为增函数.
上为增函数.
所以当x=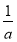 时,fmin(x)=1-ln
时,fmin(x)=1-ln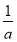 =3,解得a=e2.
=3,解得a=e2.
所以假设成立,存在实数a=e2,使得f(x)的最小值是3.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源:2015届高考苏教数学(理)训练5 函数的单调性与最值(解析版) 题型:填空题
设f(x)是定义在R上的奇函数,当x<0时,f(x)=x+ex(e为自然对数的底数),则f(ln 6)的值为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练18 同角三角函数的基本关系与诱导公式(解析版) 题型:填空题
已知α为锐角,且2tan(π-α)-3cos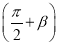 +5=0,tan(π+α)+6sin(π+β)=1,则sin α的值是______.
+5=0,tan(π+α)+6sin(π+β)=1,则sin α的值是______.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:解答题
记函数fn(x)=a·xn-1(a∈R,n∈N*)的导函数为f′n(x),已知f′3(2)=12.
(1)求a的值;
(2)设函数gn(x)=fn(x)-n2ln x,试问:是否存在正整数n使得函数gn(x)有且只有一个零点?若存在,请求出所有n的值;若不存在,请说明理由;
(3)若实数x0和m(m>0且m≠1)满足 =
= ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:填空题
已知函数f(x)=ln x+2x,若f(x2+2)<f(3x),则实数x的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
已知函数f(x)=x3+mx2+(m+6)x+1既存在极大值又存在极小值,则实数m的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练14 导数与函数单调性(解析版) 题型:解答题
已知函数f(x)=x+sin x.
(1)设P,Q是函数f(x)图像上相异的两点,证明:直线PQ的斜率大于0;
(2)求实数a的取值范围,使不等式f(x)≥axcos x在 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
曲线y=2ln x在点(e,2)处的切线(e是自然对数的底)与y轴交点的坐标为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
若命题“?x∈R,ax2-ax-2≤0”是真命题,则实数a的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com