
记函数fn(x)=a·xn-1(a∈R,n∈N*)的导函数为f′n(x),已知f′3(2)=12.
(1)求a的值;
(2)设函数gn(x)=fn(x)-n2ln x,试问:是否存在正整数n使得函数gn(x)有且只有一个零点?若存在,请求出所有n的值;若不存在,请说明理由;
(3)若实数x0和m(m>0且m≠1)满足 =
= ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.
(1)a=1 (2)存在n=1,使得函数gn(x)有且只有一个零点.
(3)见解析
【解析】【解析】
(1)f3′(x)=3ax2,由f3′(2)=12得a=1.
(2)gn(x)=xn-n2ln x-1,
g′n(x)=nxn-1-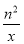 =
=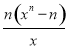 .
.
因为x>0,令gn′(x)=0得x=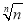 ,
,
当x>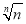 时,gn′(x)>0,gn(x)是增函数;
时,gn′(x)>0,gn(x)是增函数;
当0<x<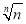 时,gn′(x)<0,gn(x)是减函数.
时,gn′(x)<0,gn(x)是减函数.
所以当x=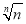 时,gn(x)有极小值,也是最小值,
时,gn(x)有极小值,也是最小值,
gn(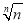 )=n-nln n-1.
)=n-nln n-1.
当x→0时,gn(x)→+∞;
当x→+∞时,gn(x)→+∞.
当n≥3时,gn(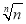 )=n(1-ln n)-1<0,函数gn(x)有两个零点;
)=n(1-ln n)-1<0,函数gn(x)有两个零点;
当n=2时,gn(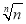 )=-2ln 2+1<0,函数gn(x)有两个零点;
)=-2ln 2+1<0,函数gn(x)有两个零点;
当n=1时,gn(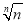 )=0,函数gn(x)有且只有一个零点.
)=0,函数gn(x)有且只有一个零点.
综上所述,存在n=1,使得函数gn(x)有且只有一个零点.
(3)fn′(x)=n·xn-1.
因为 =
= ,
,
所以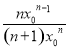 =
=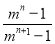 ,
,
解得x0= .
.
则x0-m= ,
,
当m>1时,(n+1)(mn-1)>0.
设h(x)=-xn+1+x(n+1)-n(x≥1),则h′(x)=-(n+1)xn+n+1=-(n+1)·(xn-1)≤0,当且仅当x=1时取等号,
所以h(x)在[1,+∞)上是减函数.
又m>1,所以h(m)<h(1)=0,
所以x0-m<0,所以x0<m.
当0<m<1时,(n+1)(mn-1)<0.
设h(x)=-xn+1+x(n+1)-n(0<x≤1),
则h′(x)=-(n+1)xn+n+1=-(n+1)·(xn-1)≥0,当且仅当x=1时取等号,所以h(x)在(0,1]上是增函数.
又因为0<m<1,所以h(m)<h(1)=0,
所以x0-m>0,所以x0>m.
综上所述,当m>1时,x0<m,当0<m<1时,x0>m.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2015届高考苏教数学(理)训练6 函数的奇偶性及周期性(解析版) 题型:填空题
已知函数f(x)是R上的奇函数,且当x>0时,f(x)=x×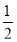 ,则f(-4)的值是________.
,则f(-4)的值是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练17 任意角和弧度制及任意角的三角函数(解析版) 题型:填空题
点P从(1,0)出发,沿单位圆逆时针方向运动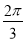 弧长到达Q点,则Q点的坐标为________.
弧长到达Q点,则Q点的坐标为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:填空题
函数f(x)=ax3+x恰有三个单调区间,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:解答题
已知函数f(x)=ax-ln x,g(x)=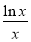 ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
(1)当a=1时,求函数f(x)的最小值;
(2)当a=1时,求证:f(m)>g(n)+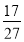 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立;
(3)是否存在实数a,使得f(x)的最小值是3?如果存在,求出a的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练1 集合(解析版) 题型:填空题
设P和Q是两个集合,定义集合P-Q={x|x∈P,且x∉Q},如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com