
分析 (1)利用递推关系式逐步求解即可.
(2)方法一:猜想通项公式,利用数学归纳法证明即可.
方法二:利用递推关系式,逐步代换求解即可;
方法三:图象数列偶数项是等差数列,奇数项是等差数列,分别求解通项公式即可.
解答 解:(1)a1=2,an+1+an=2n+3,a2=3,a3=4,a4=5;
(2)方法一:猜想an的表达式为:${a_n}=n+1({n∈{N^*}})$,
下面用数学归纳法证明:①a1=2,猜想成立;
②假设n=k(k∈N*)时,ak=k+1,则ak+1=-ak+2k+3=-(k+1)+2k+3=(k+1)+1,即n=k+1时猜想成立,
综合①②,由数学归纳法原理知:${a_n}=n+1({n∈{N^*}})$…(12分)
方法二:由an+1+an=2n+3得:${a_{n+1}}-({n+2})=-[{{a_n}-({n+1})}]=…={({-1})^n}({{a_1}-2})=0$,
所以:${a_n}=n+1({n∈{N^*}})$…(12分)
方法三:由an+1+an=2n+3得:an+2+an+1=2n+5,两式作差得:an+2-an=2,
于是a1,a3,a5,…是首项a1=2,公差为2的等差数列,那么${a_{2k-1}}=2k({k∈{N^*}})$,
且a2,a4,a6,…是首项a2=3,公差为2的等差数列,那么${a_{2k}}=2k+1({k∈{N^*}})$,
综上可知:${a_n}=n+1({n∈{N^*}})$…(12分)
点评 本题考查数列的递推关系式的应用,数列的通项公式的求法,考查转化思想以及计算能力.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | n | B. | 2n | C. | 3n | D. | 4n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
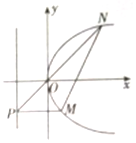 双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦点分别为F1,F2,过F2作x轴垂直的直线交双曲线C于A、B两点,△F1AB的面积为12,抛物线E:y2=2px(p>0)以双曲线C的右顶点为焦点.
双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦点分别为F1,F2,过F2作x轴垂直的直线交双曲线C于A、B两点,△F1AB的面积为12,抛物线E:y2=2px(p>0)以双曲线C的右顶点为焦点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-$\frac{1}{2}$ | B. | -$\frac{1}{2}$≤a<0 | C. | 0<a≤$\frac{1}{2}$ | D. | a≥$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com