
���� ��I���������⣬��P��x0��y0����Q��-x0��-y0������P����Բ�ϣ���${y}_{0}^{2}$=$\frac{{b}^{2}}{{a}^{2}}$��a2-${x}_{0}^{2}$����kPA•kQA=$\frac{{y}_{0}}{{x}_{0}-a}$•$\frac{{y}_{0}}{{x}_{0}+a}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-{a}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$=-$\frac{3}{4}$��c=1�����������Բ�ı����̣�
��II����ֱ��MN�ķ���Ϊx=my+1��������Բ���̣���ֱ��MA�ķ���Ϊy=$\frac{{y}_{1}}{{x}_{1}-2}$��x-2������x=3���룬yC=$\frac{{y}_{1}}{{x}_{1}-2}$=$\frac{{y}_{1}}{m{y}_{1}-1}$��ͬ��yD=$\frac{{y}_{2}}{m{y}_{2}-1}$��S1=$\frac{1}{2}$حCDح=$\frac{3}{2}$$\sqrt{{m}^{2}+1}$��S2=$\frac{1}{2}$•حAFح•حy1-y2ح=$\frac{6\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$��2S1-S2=3$\sqrt{{m}^{2}+1}$-$\frac{6\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$����$\sqrt{{m}^{2}+1}$=t��t��1������m2=t2-1��2S1-S2=3t-$\frac{6t}{3{t}^{2}+1}$���ɺ���������������t=1ʱ��ȡ��Сֵ���������2S1-S2����СֵΪ$\frac{3}{2}$��
��� �⣺��I����ԲE��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���Ľ���Ϊ2����Բ�Ľ�����x���ϣ�2c=2��c=1��
�������⣬��P��x0��y0����Q��-x0��-y0����
��P����Բ�ϣ���${y}_{0}^{2}$=$\frac{{b}^{2}}{{a}^{2}}$��a2-${x}_{0}^{2}$����
ֱ��B1A��б����ֱ��B2A��б��֮����kPA•kQA=$\frac{{y}_{0}}{{x}_{0}-a}$•$\frac{{y}_{0}}{{x}_{0}+a}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-{a}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$��
��������$\frac{{b}^{2}}{{a}^{2}}$=$\frac{3}{4}$��
��c=1��
��a2=4��b2=3��
����ԲE�ķ���Ϊ��$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��II����ֱ��MN�ķ���Ϊx=my+1����M��x1��y1����N��x2��y2����
$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$�������ã�3m2+4��y2+6my-9=0��
��Τ�ﶨ��֪��y1+y2=-$\frac{6m}{3{m}^{2}+4}$��y1•y2=-$\frac{9}{3{m}^{2}+4}$��
��ֱ��MA�ķ���Ϊy=$\frac{{y}_{1}}{{x}_{1}-2}$��x-2������x=3���룬
��yC=$\frac{{y}_{1}}{{x}_{1}-2}$=$\frac{{y}_{1}}{m{y}_{1}-1}$��ͬ��yD=$\frac{{y}_{2}}{m{y}_{2}-1}$��
��حCDح=حyC-yDح=$\frac{ح{y}_{1}-{y}_{2}ح}{{m}^{2}{y}_{1}{y}_{2}-m��{y}_{1}+{y}_{2}��+1}$=3$\sqrt{{m}^{2}+1}$��
��S1=$\frac{1}{2}$حCDح=$\frac{3}{2}$$\sqrt{{m}^{2}+1}$��S2=$\frac{1}{2}$•حAFح•حy1-y2ح=$\frac{6\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$��
��2S1-S2=3$\sqrt{{m}^{2}+1}$-$\frac{6\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$��
��$\sqrt{{m}^{2}+1}$=t��t��1������m2=t2-1��
2S1-S2=3t-$\frac{6t}{3{t}^{2}+1}$��
��f��t��=3t-$\frac{6t}{3{t}^{2}+1}$����f�䣨t��=3+$\frac{6��3{t}^{2}-1��}{��3{t}^{2}+1��^{2}}$��0��
��f��t����[1��+�ޣ������������Ӷ�f��t������СֵΪf��1��=$\frac{3}{2}$��
��2S1-S2����СֵΪ$\frac{3}{2}$��
���� ���⿼����Բ�ı����̼��������ʣ�����ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�����ҳ���ʽ�������ε������ʽ��Ӧ�ã�����Բ�����뵼�����ۺ�Ӧ�ã�������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| X | 1 | 2 | 3 |
| P | 0.5 | x | y |
| A�� | $\frac{7}{32}$ | B�� | $\frac{9}{32}$ | C�� | $\frac{33}{64}$ | D�� | $\frac{55}{64}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��2�� | B�� | [-1��2�� | C�� | ��-�ޣ�-1] | D�� | {-1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
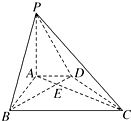 ��ͼ���ڵ���Ϊֱ�����ε�����P-ABCD�У�AD��BC����ABC=90�㣬PA��ƽ��ABCD��PA=3��AD=2��AB=2$\sqrt{3}$��BC=6��
��ͼ���ڵ���Ϊֱ�����ε�����P-ABCD�У�AD��BC����ABC=90�㣬PA��ƽ��ABCD��PA=3��AD=2��AB=2$\sqrt{3}$��BC=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
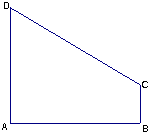 ��ͼ����ֱ������ABCD�У���BAD=90�㣬AD��BC��AB=2��AD=$\frac{3}{2}$��BC=$\frac{1}{2}$����Բ��A��BΪ�����Ҿ�����D��
��ͼ����ֱ������ABCD�У���BAD=90�㣬AD��BC��AB=2��AD=$\frac{3}{2}$��BC=$\frac{1}{2}$����Բ��A��BΪ�����Ҿ�����D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com