练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数y=f(x)在(-∞,+ ∞)内有定义,对于给定的正数k,定义函数fk(x)= 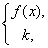 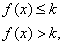设函数f(x)=2+x-ex,若对任意的x∈(-∞,+ ∞)恒有fk(x)=f(x),则(   )

    A.k的最大值为2                       B.k的最小值为2

    C.k的最大值为1                       D.k的最小值为1


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知命题P：“存在命题：“中，若则。则下列命题为真命题的是                                     （    ）

    A．       B．      C．        D． 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列函数中，既是奇函数又是增函数的为（   ）

    A.     B.       C.         D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


      已知函数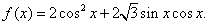

    (１)求函数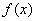的单调递减区间．

    (２)将函数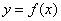的图像向左平移个单位,再将所得图像上各点的横坐标缩短为原来的倍,纵坐标不变,得到函数的图像.求在上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    平面内两定点A、B及动点P，设命题甲是：“|PA|+|PB|是定值”，命题乙是：“点P的轨迹是以A．B为焦点的椭圆”，那么（    ）

    A．甲是乙成立的充分不必要条件        B．甲是乙成立的必要不充分条件

    C．甲是乙成立的充要条件                 D．甲是乙成立的非充分非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下图是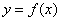函数的导函数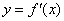的图象，下列说法正确的是___________．  

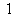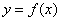    ①．是函数的极值点；

    ②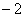．是函数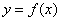的极小值点

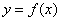    ③．在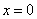处切线的斜率大于零；

    ④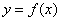．在区间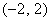上单调递增.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设，则等于（     ）.

     A．     B          C．         D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设函数，曲线过P（1,0），且在P点处的切斜线率为2．

    （I）求a，b的值；（II）证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知集合,,

    （1）求,;（2）若,求a的取值范围.

    查看答案和解析>>

    同步练习册答案