
【题目】记所有非零向量构成的集合为V,对于 ![]() ,
, ![]() ∈V,
∈V, ![]() ≠
≠ ![]() ,定义V(
,定义V( ![]() ,
, ![]() )=|x∈V|x
)=|x∈V|x ![]() =x
=x ![]() |
|
(1)请你任意写出两个平面向量 ![]() ,
, ![]() ,并写出集合V(
,并写出集合V( ![]() ,
, ![]() )中的三个元素;
)中的三个元素;
(2)请根据你在(1)中写出的三个元素,猜想集合V( ![]() ,
, ![]() )中元素的关系,并试着给出证明;
)中元素的关系,并试着给出证明;
(3)若V( ![]() ,
, ![]() )=V(
)=V( ![]() ,
, ![]() ),其中
),其中 ![]() ≠
≠ ![]() ,求证:一定存在实数λ1 , λ2 , 且λ1+λ2=1,使得
,求证:一定存在实数λ1 , λ2 , 且λ1+λ2=1,使得 ![]() =λ1
=λ1 ![]() +λ2
+λ2 ![]() .
.
【答案】
(1)解:比如 ![]() =(1,2),
=(1,2), ![]() =(3,4),设
=(3,4),设 ![]() =(x,y),
=(x,y),
由 ![]()
![]() =
= ![]()
![]() ,可得x+2y=3x+4y,
,可得x+2y=3x+4y,
即为x+y=0,
则集合V( ![]() ,
, ![]() )中的三个元素为(1,﹣1),(2,﹣2),(3,﹣3)
)中的三个元素为(1,﹣1),(2,﹣2),(3,﹣3)
(2)解:由(1)可得这些向量共线.
理由:设 ![]() =(s,t),
=(s,t), ![]() =(a,b),
=(a,b), ![]() =(c,d),
=(c,d),
由 ![]()
![]() =
= ![]()
![]() ,可得as+bt=cs+dt,
,可得as+bt=cs+dt,
即有s= ![]() t,
t,
即 ![]() =(
=( ![]() t,t),
t,t),
故集合V( ![]() ,
, ![]() )中元素的关系为共线
)中元素的关系为共线
(3)解:证明:设 ![]() =(s,t),
=(s,t), ![]() =(a,b),
=(a,b), ![]() =(c,d),
=(c,d),
![]() =(u,v),
=(u,v), ![]() =(e,f),
=(e,f),
若V( ![]() ,
, ![]() )=V(
)=V( ![]() ,
, ![]() ),
),
即有as+bt=cs+dt,au+bv=ue+fv,
解得a= ![]() c+
c+ ![]() e+
e+ ![]() ,
,
可令d=f,可得λ1= ![]() ,
,
λ2= ![]() ,
,
则一定存在实数λ1,λ2,且λ1+λ2=1,使得 ![]() =λ1
=λ1 ![]() +λ2
+λ2 ![]()
【解析】(1)比如 ![]() =(1,2),
=(1,2), ![]() =(3,4),设
=(3,4),设 ![]() =(x,y),运用数量积的坐标表示,即可得到所求元素;(2)由(1)可得这些向量共线.理由:设
=(x,y),运用数量积的坐标表示,即可得到所求元素;(2)由(1)可得这些向量共线.理由:设 ![]() =(s,t),
=(s,t), ![]() =(a,b),
=(a,b), ![]() =(c,d),运用数量积的坐标表示,以及共线定理即可得到;(3)设
=(c,d),运用数量积的坐标表示,以及共线定理即可得到;(3)设 ![]() =(s,t),
=(s,t), ![]() =(a,b),
=(a,b), ![]() =(c,d),
=(c,d), ![]() =(u,v),
=(u,v), ![]() =(e,f),运用新定义和数量积的坐标表示,解方程可得a,即可得证.
=(e,f),运用新定义和数量积的坐标表示,解方程可得a,即可得证.


科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足:对任意的x1 , x2∈(﹣∞,0)(x1≠x2),都有 ![]() <0.则下列结论正确的是( )
<0.则下列结论正确的是( )
A.f(0.32)<f(20.3)<f(log25)
B.f(log25)<f(20.3)<f(0.32)
C.f(log25)<f(0.32)<f(20.3)
D.f(0.32)<f(log25)<f(20.3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列推理中属于归纳推理且结论正确的是( )
A.由an=2n﹣1,求出S1=12 , S2=22 , S3=32 , …,推断:数列{an}的前n项和Sn=n2
B.由f(x)=xcosx满足f(﹣x)=﹣f(x)对?x∈R都成立,推断:f(x)=xcosx为奇函数
C.由圆x2+y2=r2的面积S=πr2 , 推断:椭圆 ![]() =1的面积S=πab
=1的面积S=πab
D.由(1+1)2>21 , (2+1)2>22 , (3+1)2>23 , …,推断:对一切n∈N* , (n+1)2>2n
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如表为“五点法”绘制函数f(x)=Asin(ωx+φ)图象时的五个关键点的坐标(其中A>0,ω>0,|φ|<π)
x | ﹣ |
|
|
|
|
f(x) | 0 | 2 | 0 | ﹣2 | 0 |
(Ⅰ)请写出函数f(x)的最小正周期和解析式;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的导函数为
的导函数为![]() .
.
⑴ 若直线![]() 与曲线
与曲线![]() 恒相切于同一定点,求
恒相切于同一定点,求![]() 的方程;
的方程;
⑵ 若![]() ,求证:当
,求证:当![]() 时,
时, ![]() 恒成立;
恒成立;
⑶ 若当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中, ![]() ,前
,前![]() 项和
项和![]() 满足
满足![]() (
(![]() ).
).
⑴ 求数列![]() 的通项公式;
的通项公式;
⑵ 记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
⑶ 是否存在整数对![]() (其中
(其中![]() ,
, ![]() )满足
)满足![]() ?若存在,求出所有的满足题意的整数对
?若存在,求出所有的满足题意的整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
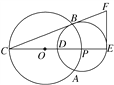
【题目】如图,圆O与圆P相交于A,B两点,圆心P在圆O上,圆O的弦BC切圆P于点B,CP及其延长线交圆P于D,E两点,过点E作EF⊥CE,交CB的延长线于点F.
(1)求证:B,P,E,F四点共圆;
(2)若CD=2,CB=2![]() ,求出由B,P,E,F四点所确定的圆的直径.
,求出由B,P,E,F四点所确定的圆的直径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海关对同时从A、B、C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
地区 | A | B | C |
数量 | 50 | 150 | 100 |
(1)求这6件样品中来自A、B、C各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com