
分析 结合函数的性质作函数y=f(x)的部分图象,将[1,2n]分割成[1,2],[2,4],[4,8],[8,16],…,[2n-1,2n]个部分,从而可得各部分的面积,从而求和即可.
解答 解:∵f(2x)=2f(x),当1≤x≤2时,f(x)=$\frac{1}{2}$-|x-$\frac{3}{2}$|,
∴作函数y=f(x)的部分图象如下图,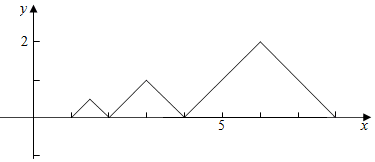 ,
,
将[1,2n]分割成[1,2],[2,4],[4,8],[8,16],…,[2n-1,2n]个部分,
设在各区间内的面积依次为a1,a2,a3,…,an;
则结合图象可得,a1=$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$,an=4an-1,
故S1=a1=$\frac{1}{4}$,Sn=$\frac{\frac{1}{4}(1-{4}^{n})}{1-4}$=$\frac{1}{12}$(4n-1),
故答案为:$\frac{1}{4}$,$\frac{1}{12}$(4n-1).
点评 本题考查了分段函数与绝对值函数的应用及转化思想与分类讨论及数形结合的思想应用,同时考查了数列的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-1,1) | C. | (-1,0) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
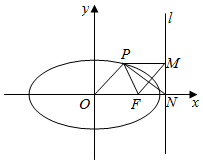 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点为F,右准线l交x轴于点N,过椭圆上一点P作PM垂直于准线l,垂足为M,若PN平分∠FPM,且四边形OFMP为平行四边形.证明:e$>\frac{2}{3}$.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点为F,右准线l交x轴于点N,过椭圆上一点P作PM垂直于准线l,垂足为M,若PN平分∠FPM,且四边形OFMP为平行四边形.证明:e$>\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | [$\frac{4}{3}$,+∞) | D. | [1,$\frac{4}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
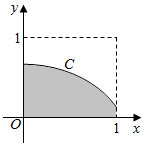 在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )| A. | 3413 | B. | 1193 | C. | 2718 | D. | 6587 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com