
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
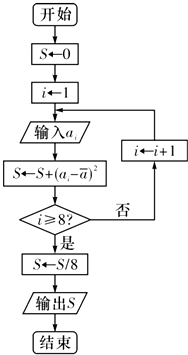 对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.
对一个作直线运动的质点的运动过程观测了8次,得到如表所示的数据.| 观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 观测数据ai | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
. |
| a |
| A、5 | B、6 | C、7 | D、8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:| 幸福感指数 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
| 男市民人数 | 10 | 20 | 220 | 125 | 125 |
| 女市民人数 | 10 | 10 | 180 | 175 | 125 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 4 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com