
【题目】一个袋子里装有7个球,其中有红球4个,编号分别为1,2,3,4;白球3个,编号分别为2,3,4.从袋子中任取4个球(假设取到任何一个球的可能性相同).
(Ⅰ)求取出的4个球中,含有编号为3的球的概率;
(Ⅱ)在取出的4个球中,红球编号的最大值设为X,求随机变量X的分布列和数学期望.
【答案】解:(Ⅰ) 设“取出的4个球中,含有编号为3的球”为事件A,则 ![]()
所以,取出的4个球中,含有编号为3的球的概率为 ![]() .
.
(Ⅱ)随机变量X的所有可能取值为1,2,3,4.… ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以随机变量X的分布列是
X | 1 | 2 | 3 | 4 |
P |
|
|
|
|
随机变量X的数学期望 ![]() .
.
【解析】(I)先求出7个球中取出4个球的种数,再求出取出的4个球中,含有编号为3的球的种数,最后利用古典概型的概率公式可得取出的4个球中,含有编号为3的球的概率;(II)先分别求出随机变量的所有可能取值的概率,再写出分布列,进而可得数学期望.
【考点精析】关于本题考查的离散型随机变量及其分布列,需要了解在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量A与B的随机变量K2越大,说明“A与B有关系”的可信度越大.
②以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=lny,将其变换后得到线性方程z=0.3x+4,则c,k的值分别是e4和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为y=a+bx中,b=1, ![]() =1,
=1, ![]() =3,
=3,
则a=1.正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当![]() 时,函数
时,函数![]() 的值域是_________.
的值域是_________.
【答案】[-1,2]
【解析】:f(x)=sinx+![]() cosx=2(
cosx=2(![]() sinx+
sinx+![]() cosx)=2sin(x+
cosx)=2sin(x+![]() ),
),
∵﹣![]() ≤x≤
≤x≤![]() ,
,
∴﹣![]() ≤x+
≤x+![]() ≤
≤![]() ,
,
∴﹣![]() ≤sin(x+
≤sin(x+![]() )≤1,
)≤1,
∴函数f(x)的值域为[﹣1,2],
故答案为:[﹣1,2].
【题型】填空题
【结束】
15
【题目】若点O在![]() 内,且满足
内,且满足![]() ,设
,设![]() 为
为![]() 的面积,
的面积, ![]() 为
为![]() 的面积,则
的面积,则![]() =________.
=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,设函数
,设函数![]() .
.
(1)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且
对称,且![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)在(1)的条件下,当![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=6cos2![]() +
+![]() sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.

(1)求ω的值及函数f(x)的值域;
(2)若f(x0)=![]() ,且x0∈(-
,且x0∈(-![]() ,
,![]() ),求f(x0+1)的值.
),求f(x0+1)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]()
(1)判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)判断并证明函数![]() 在
在![]() 上的单调性;
上的单调性;
(3)是否存在这样的负实数![]() ,使
,使![]() 对一切
对一切![]() 恒成立,若存在,试求出
恒成立,若存在,试求出![]() 取值的集合;若不存在,说明理由
取值的集合;若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分别为SA,SB的中点,E为CD中点,过M,N作平面MNPQ分别与BC,AD交于点P,Q,若 ![]() =t
=t ![]() .
. 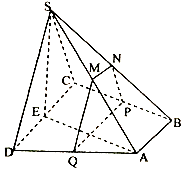
(1)当t= ![]() 时,求证:平面SAE⊥平面MNPQ;
时,求证:平面SAE⊥平面MNPQ;
(2)是否存在实数t,使得二面角M﹣PQ﹣A的平面角的余弦值为 ![]() ?若存在,求出实数t的值;若不存在,说明理由.
?若存在,求出实数t的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1 , AB⊥AN,CB=BA=AN= ![]() BB1 .
BB1 . 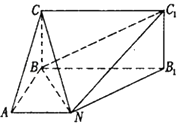
(1)求证:BN⊥平面C1B1N;
(2)求二面角C﹣C1N﹣B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com