解:

①求出f′(x)=x
2+2bx+c;
∴f′(1)=1+2b+c=0?b=
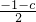
且f′(m)=m
2+(-1-c)m+c=-1;
∴m
2-(1+c)m+c+1=0,
∴△=(1+c)
2-4(1+c)≥0,则c≥3或c≤-1;
又∵b=
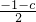
<1
∴c>-3;又b=
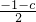
>c,则有c<

,∴-3<c≤-1.…(4分)
②f′(x)=x
2+(-1-c)x+c=(x-c) (x-1),
其图象开口向上,对称轴为:-1<x
0=
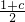
<0;
∵f′(m)=-1<0,
∴-3<c<m<1;
则-7<m-4<-3?f′(m-4)>0;…(9分)
③由于f′(m-4)>0;
∵函数f(x)在x=1处取到一个极小值,
∴函数f(x)在(-∞,c)和(1,+∞)上为增函数,在(c,1)上为减函数,
∴m-4≤c,
f(x)在x∈[m-4,1]上的最大值等于f(c)=

c
3+

•c
2+c
2=
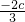
,
∴c=-1,或c=4(舍去);
由f′(m)=-1,可得m=0,则f(x)=

x
3-x,(x∈[-4,1])
∴函数的最小值为f(-4)=
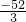
.…(13分)
分析:①存在实数m,使f′(m)=-1,得到关于m的一元二次方程有实数根,用根的判别式列出关于b、c的不等式,结合函数在x=1处取到极小值,说明f′(1)=0,消去b得到关于c的一元二次不等式,最后结合c<b<1解出c取值范围.
②函数的导数是关于x的二次函数,其图象开口向上,在区间(c,1)上取值为负,而f′(m)=-1为负,得到-3<c<m<1,从而得到-7<m-4<-3,因此f′(m-4)的符号为正.
③由②f′(m-4)>0且在x=1时函数f(x)取到极小值,得到函数f(x)的单调性:在(-∞,c)和(1,+∞)上为增函数,在(c,1)上为减函数.因此m-4≤c,f(x)在x∈[m-4,1]上的最大值为f(c),从而解出c=-1且m=0,得出函数的表达式为f(x)=

x
3-x,最后可得f(x)在x∈[-4,1]上的最小值.
点评:本题考查了利用导数研究函数的极值、函数在某点取得极值的条件和得用导数求闭区间上函数的最值等知识点,属于中档题.

 x3+bx2+cx(c<b<1)在x=1处取到一个极小值,且存在实数m,使f′(m)=-1,
x3+bx2+cx(c<b<1)在x=1处取到一个极小值,且存在实数m,使f′(m)=-1,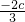 ,求f(x)在x∈[m-4,1]上的最小值.
,求f(x)在x∈[m-4,1]上的最小值. ①求出f′(x)=x2+2bx+c;
①求出f′(x)=x2+2bx+c;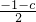 且f′(m)=m2+(-1-c)m+c=-1;
且f′(m)=m2+(-1-c)m+c=-1;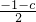 <1
<1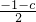 >c,则有c<
>c,则有c< ,∴-3<c≤-1.…(4分)
,∴-3<c≤-1.…(4分)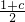 <0;
<0; c3+
c3+ •c2+c2=
•c2+c2=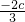 ,
, x3-x,(x∈[-4,1])
x3-x,(x∈[-4,1])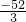 .…(13分)
.…(13分) x3-x,最后可得f(x)在x∈[-4,1]上的最小值.
x3-x,最后可得f(x)在x∈[-4,1]上的最小值.

 名题金卷系列答案
名题金卷系列答案