分析:方法一:(I)如图,由线面角的定义作出直线C1B与底面ABC所成角,在直角三角形中求出该角的正切值.
(II)由图形及题设可观察出当E为中点时,EA⊥EB1.下由线面垂直来证线线垂直.
(III)先做出二面角的平面角,再进行证明,然后再求角.
方法二:建立空间坐标系,给出各点的坐标,(I)求出面的法向量与线的方向向量,由公式求线面角.
(II)设出E的坐标,将垂直关系转化为向量的内积为零建立方程求E的坐标.即可确定出E的位置.
(III)求出两面的法向量,再由公式求出二面角的余弦值.
解答:解:(1)在直三棱柱ABC-A
1B
1C
1中,CC
1⊥平面ABC,
∴C
1B在平面ABC上的射影为CB.
∴∠C
1BC为直线C
1B与底面ABC所成角.
∵CC
1=BB
1=2,BC=1,∴tan∠C
1BC=2.
即直线C
1B与底面ABC所成角正切值为2.
(2)当E为中点时,EA⊥EB
1.
∵CE=EC
1=1,BC=B
1C
1=1,∴∠BEC=∠B
1EC
1=45
0,∴∠BEB
1=90°,
即B
1E⊥BE
又∵AB⊥平面BB
1CC
1,EB
1?平面BB
1C
1C∴AB⊥EB
1,
∵BE∩AB=B,∴EB
1⊥平面ABE,
EA?平面ABE,EA⊥EB
1.

(3)取EB
1的中点G,A
1E的中点F,
则FG∥A
1B
1,且FG=
A
1B
1,
∵A
1B
1⊥EB
1,∴FG⊥EB
1,
连接A
1B,AB
1,设A
1B∩AB
1=O,
连接OF,OG,FG,
则OG∥AE,且OG=
AE,∵AE⊥EB
1,∴OG⊥EB
1.
∴∠OGF为二面角A-EB
1-A
1的平面角.
∵OG=
AE=1,且FG=
A
1B
1=
,OF=
BE=
,∠OGF=45°
∴二面角A-EB
1-A
1的大小为45°,
另解:如图,以B为原点建立空间直角坐标系,则B(0,0,0),C
1(1,2,0),B
1(0,2,0).
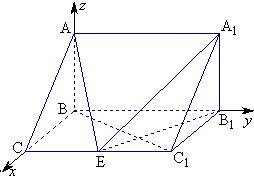
(1)直三棱柱ABC-A
1B
1C
1中,
平面ABC的法向量
=(0,2,0).,
又
=(1,2,0)
设C
1B与平面ABC所成的角为θ,
则sinθ=|cos
<,>|=
∴tanθ=2
即直线C
1B与底面ABC所成角正切值为2.
(2)设E(1,y,0),则
=(-1,2-y,0),
=(-1,y,z)
∵AE⊥EB
1,∴AE•EB
1=1-y(2-y)=0
∴y=1,即E(1,1,0),∴E为CC
1的中点.
(3)∵A(0,0,2),则
=(1,1,-
),
=(1,-1,0),
设平面AEB
1的法向量
=(x
1,y
1,z
1),
则
∴
,取
=(1,1,
)
∵
=(1,-1,0),
,
•=1-1=0∴BE⊥B
1E,
又BE⊥A
1B
1,∴BE⊥平面A
1B
1E,∴平面A
1B
1E的法向量
=(1,1,0),∴cos<
,
>=
∴二面角A-EB
1-A
1的大小为45°.
点评:考查线面角的求法,线线垂直的证明以及二面角的求法,方法二中用空间向量求线面角,证线线垂直,求二面角,方法新颖.

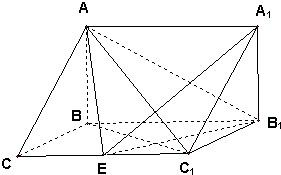 如图,在三棱柱ABC-中,已知CC1=BB1=2,BC=1,∠BCC1=
如图,在三棱柱ABC-中,已知CC1=BB1=2,BC=1,∠BCC1= (3)取EB1的中点G,A1E的中点F,
(3)取EB1的中点G,A1E的中点F, (1)直三棱柱ABC-A1B1C1中,
(1)直三棱柱ABC-A1B1C1中,

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( ) 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.