[题目]若动圆与圆外切.且与直线相切.则动圆圆心的轨迹方程是( )A. B. C. D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】若动圆与圆外切，且与直线相切，则动圆圆心的轨迹方程是（）

A. B. C. D.

【答案】C

【解析】

令动圆圆心P的坐标为（x，y），C1（5，0），动圆得半径为r，则根据两圆相外切及直线与圆相切得性质可得P（x，y）到C1（5，0）与直线x＝5的距离相等，由抛物线定义可求．

设圆圆的圆心C1（5，0），动圆圆心P的（x，y），半径为r，

作x＝，x＝3，PQ⊥直线x＝5，Q为垂足，因圆P与x＝3相切，故圆P到直线x＝的距离PQ＝r+2，又PC1＝r+2，

因此P（x，y）到C1（5，0）与直线x＝的距离相等，P的轨迹为抛物线，焦点为C1（5，0），准线x＝，

顶点为（0，0），

开口向右，可得P＝10，方程为：．

故选：C．

练习册系列答案

练习册吉林教育出版集团有限责任公司系列答案

应用题天天练东北师范大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设：实数满足，：实数满足.

（1）若，且为真，求实数的取值范围；

（2）若，且是的充分不必要条件，求实数的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知抛物线x2=4y．

（1）求抛物线在点P（2，1）处的切线方程；

（2）若不过原点的直线l与抛物线交于A，B两点（如图所示），且OA⊥OB，|OA|=|OB|，求直线l的斜率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥中，底面为矩形，平面，,为的中点，是线段上的一动点．

（1）当是线段的中点时，证明：平面；

（2）当求二面角的大小．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某学校微信公众号收到非常多的精彩留言,学校从众多留言者中抽取了100人参加“学校满意度调查”,其留言者年龄集中在之间,根据统计结果,做出频率分布直方图如下:

(1)求这100位留言者年龄的平均数和中位数;

(2)学校从参加调查的年龄在和的留言者中,按照分层抽样的方法,抽出了6人参加“精彩留言”经验交流会,赠与年龄在的留言者每人一部价值1000元的手机,年龄在的留言者每人一套价值700元的书,现要从这6人中选出3人作为代表发言,求这3位发言者所得纪念品价值超过2300元的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在如图所示的多面体中，已知，，是正三角形，，，是的中点.

（1）求证：平面；

（2）求证：平面平面；

（3）求到平面的距离.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某省为了确定合理的阶梯电价分档方案，对全省居民用量进行了一次抽样调查，得到居民月用电量（单位：度）的频率分布直方图（如图所示），求：

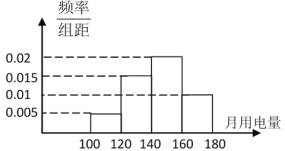
（1）若要求80%的居民能按基本档的电量收费，则基本档的月用电量应定为多少度？

（2）由频率分布直方图可估计，居民月用电量的众数、中位数和平均数分别是多少？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】4月16日摩拜单车进驻大连市旅顺口区，绿色出行引领时尚，旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计，若将单车用户按照年龄分为“年轻人”(20岁～39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类，抽取一个容量为200的样本，将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”，已知“经常使用单车用户”有120人，其中是“年轻人”，已知“不常使用单车用户”中有是“年轻人”.